Как работает цап – Цифро-аналоговый преобразователь — Википедия — Заработок в сети Интернет. Как заработать на дому в Интернете. Удаленная работа в сети.

Содержание

Цифроаналоговые преобразователи (ЦАП), принцип работы, типы

Цифроаналоговые преобразователи (ЦАП) — предназначены для преобразования цифровых сигналов в аналоговые. Такое преобразование необходимо, например, при восстановлении аналогового сигнала, предварительно преобразованного в цифровой для передачи на большое расстояние или хранения (таким сигналом, в частности, может быть звук). Другой пример использования такого преобразования — получение управляющего сигнала при цифровом управлении устройствами, режим работы которых определяется непосредственно аналоговым сигналом (что, в частности, имеет место при управлении двигателями).

{xtypo_quote}К основным параметрам ЦАП относят разрешающую способность, время установления, погрешность нелинейности и др.{/xtypo_quote}

Разрешающая способность — величина, обратная максимальному числу шагов квантования выходного аналогового сигнала. Время установления t_уст — интервал времени от подачи кода на вход до момента, когда выходной сигнал войдет в заданные пределы, определяемые погрешностью. Погрешность нелинейности — максимальное отклонение графика зависимости выходного напряжения от напряжения, задаваемого цифровым сигналом, по отношению к идеальной прямой во всем диапазоне преобразования.

Как и рассматриваемые аналого-цифровые преобразователи (АЦП), ЦАП являются «связующим звеном» между аналоговой и цифровой электроникой. Существуют различные принципы построения АЦП.

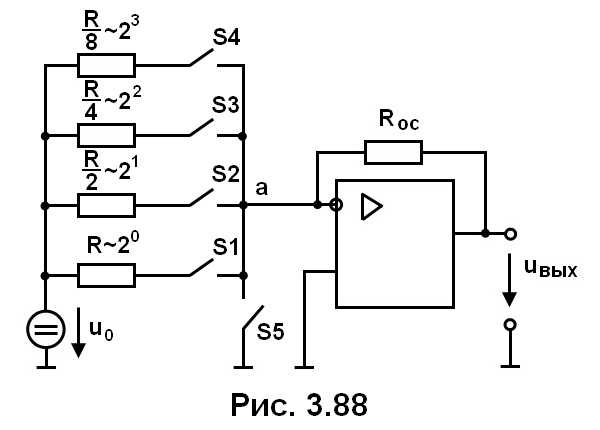
Схема ЦАП с суммированием весовых токов

На рис. 3.88 приведена схема ЦАП с суммированием весовых токов.

Ключ S₅ замкнут только тогда, когда разомкнуты все ключи S₁…S₄ (при этом u_вых= 0). U₀

— опорное напряжение. Каждый резистор во входной цепи соответствует определенному разряду двоичного числа.

По существу этот ЦАП — инвертирующий усилитель на основе операционного усилителя. Анализ такой схемы не представляет затруднений. Так, если замкнут один ключ

S1, то u_вых= −U₀R_oc/ R

что соответствует в первом и нулям в остальных разрядах.

Из анализа схемы следует, что модуль выходного напряжения пропорционален числу, двоичный код которого определяется состоянием ключей S₁…S₄. Токи ключей S₁…S₄ суммируются в точке «а», причем токи различных ключей различны (имеют разный «вес»). Это и определяет название схемы.

Из вышеизложенного следует, что u_вых= − ( U₀R_oc/ R ) · S₁ − ( U₀R_oc/ (R/2) ) · S₂ – − ( U₀R_oc/ (R/4) ) · S₃− ( U₀R_oc/ (R/8) ) · S₄ = = − ( U₀R_oc/ R ) · ( 8S₄ + 4S₃ + 2S₂+ S₁)

где S_i ,i = 1, 2, 3, 4 принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.

Состояние ключей определяется входным преобразуемым кодом. Схема проста, но имеет недостатки: значительные изменения напряжения на ключах и использование резисторов с сильно отличающимися сопротивлениями. Требуемую точность этих сопротивлений обеспечить затруднительно.

ЦАП на основе резистивной матрицы R — 2R

Рассмотрим ЦАП на основе резистивной матрицы R — 2R(матрицы постоянного сопротивления) (рис. 3.89).

В схеме использованы так называемые перекидные ключи S₁…S₄, каждый из которых в одном из состояний подключен к общей точке, поэтому напряжения на ключах невелики. Ключ S₅ замкнут только тогда, когда все ключи S₁…S₄ подключены к общей точке. Во входной цепи использованы резисторы всего с двумя различными значениями сопротивлений.

Из анализа схемы можно увидеть, что и для нее модуль выходного напряжения пропорционален числу, двоичный код которого определяется состоянием ключей S₁…S₄. Анализ легко выполнить, учитывая следующее. Пусть каждый из ключей S₁…S₄ подключен к общей точке. Тогда, как легко заметить, напряжение относительно общей точки в каждой следующей из точек «a»…«d» в 2 раза больше, чем в предыдущей. К примеру, напряжение в точке «b» в 2 раза больше, чем в точке «а» (напряжения U_а, U_b, U_c и U_d в указанных точках определяются следующим образом:

U_a = U₀

U_c = U₀ / 2

U_b = U₀ / 4

U_d = U₀ / 8

Допустим, что состояние указанных ключей изменилось. Тогда напряжения в точках «a»…«d» не изменятся, так как напряжение между входами операционного усилителя практически нулевое.

Из вышеизложенного следует, что:

u_вых= − ( U₀R_oc/ 2R ) · S₄ − ( (U₀/2) R_oc/ 2R ) · S₃ – ( (U₀/4) R_oc/ 2R ) · S₂− ( (U₀/8) R_oc/ 2R ) · S₁ = − ( U₀R_oc/ 16R) · ( 8S₄+ 4S₃+ 2S₂+ S₁)

где S_i, i = 1, 2, 3, 4 принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.

ЦАП для преобразования двоично-десятичных чисел

Рассмотрим ЦАП для преобразования двоично-десятичных чисел (рис. 3.90).

Для представления каждого разряда десятичного числа используется отдельная матрица R − 2R (обозначены прямоугольниками). Z₀…Z₃ обозначают числа, определенные состоянием ключей каждой матрицы R − 2R. Принцип действия становится понятным, если учесть, что сопротивление каждой матрицы R, и если выполнить анализ фрагмента схемы, представленного на рис. 3.91. 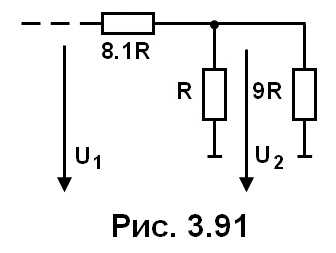Из анализа следует, что

U₂ = U₁ · [ ( R||9R) / (8,1R + R||9R) ]

R||9R = (R · 9R) / (R + 9R) = 0,9R

Следовательно, U₂ = 0,1 U₁. С учетом этого получим

u_вых= − ( U₀R_oc/ 16R ) · 10⁻³ ( 10³ · Z₃ + 10² · Z₂ + 10 · Z₁+ Z₀)

Наиболее распространенными являются ЦАП серий микросхем 572, 594, 1108, 1118 и др. В табл. 3.2 приведены…

Параметры некоторых ЦАП

pue8.ru

ЦАП. Так ли все просто?

Цифро-аналоговый преобразователь — устройство для перевода цифровых данных в аналоговый сигнал. Это своеобразный мост между аналоговой и цифровой частями схемы. Сфера применения ЦАП очень широка. Это — усилители звука, аудиокодеки, обработка видео, устройства отображения, системы распознавания данных, калибровка датчиков и других измерительных устройств, схемы управления двигателями, системы распределения данных, цифровые потенциометры, программируемое радио (SDR) и т.д.

Принцип работы

Принцип работы ЦАП заключается в суммировании аналоговых сигналов (ток или напряжение). Суммирование производится с коэффициентами, равными нулю или единице в зависимости от значения соответствующего разряда кода. Выходной сигнал ЦАП может иметь форму тока, напряжения или заряда. Преобразователи с токовым выходом используются в основном в прецизионных и высокочастотных схемах. Для определенности мы будем рассматривать ЦАП с выходным напряжением, как наиболее распространенные. Из таблицы 1 видно, что максимальное выходное напряжение на 1 МЗР (младший значащий разряд входного кода) ниже напряжения полной шкалы (ПШ). Некоторые ЦАП позволяют использовать всю шкалу.

Табл. 1. Сигналы четырехразрядного ЦАП (опорное напряжение 5 В)

Входной код	Выходное напряжение, В
0000	0,0000
0001	0,3125
0010	0,6250
0011	0,9375
0100	1,2500
0101	1,5625
0110	1,8750
0111	2,1875
1000	2,5000
1001	2,8125
1010	3,1250
1011	3,4375
1100	3,7500
1101	4,0625
1110	4,3750
1111	4,6875

Характеристики ЦАП

Наиболее важные характеристики ЦАП — это разрядность, шаг квантования (разрешающая способность) и точность преобразования.

Передаточная характеристика (ПХ) — зависимость выходного сигнала ЦАП от входных данных.

Разрядность (N) — количество бит во входном коде.

Разрешение — это выходное напряжение, соответствующее 1 МЗР. Оно зависит от количества разрядов и определяет точность преобразования сигнала.

Частота дискретизации (частота Найквиста) — максимальная частота, на которой ЦАП может работать, выдавая на выходе корректный результат. В соответствии с теоремой Котельникова, для корректного воспроизведения аналогового сигнала из цифровой формы необходимо, чтобы частота дискретизации была не меньше удвоенной максимальной частоты в спектре сигнала.

Полная шкала — диапазон значений выходного сигнала.

Монотонность — участок на ПХ, где наклон постоянен. На этом участке ЦАП линеен.

Время установления — интервал времени от момента изменения входного кода до окончательного вхождения выходного сигнала в заданный диапазон отклонения.

Выходной выброс — это переходный процесс, возникающий во время смены входных данных. Величина выброса зависит от количества переключаемых разрядов.

Погрешность смещения нуля — разность между фактическим и идеальным выходным сигналом, когда на входе ноль.

Погрешность ПШ — разница между фактическим выходным напряжением и напряжением ПШ.

Погрешность усиления — отклонение наклона ПХ от идеального.

Дифференциальная нелинейность — разность приращений выходных сигналов, соответствующих смежным соседним кодам.

Интегральная нелинейность — максимальное отклонение реальной ПХ от прямой линии.

Классификация

Цифро-аналоговые преобразователи делятся по типу входных данных на последовательные и параллельные. По разрядности выделяют ЦАП с повышенной точностью (большая разрядность, N≥14) или с высоким быстродействием (6—8 разрядов). Выходной сигнал может иметь форму напряжения, тока или заряда.

Рассмотрим некоторые структуры ЦАП. Простейшим ЦАП является взвешивающий (делитель Кельвина), структура которого показана на рисунке 1. Каждому биту преобразуемого двоичного кода соответствует резистор или источник тока, подключенный на общую точку суммирования. Сила тока источника (или проводимость резистора) пропорциональна весу бита, которому он соответствует. N-разрядный ЦАП содержит 2N одинаковых последовательно соединенных резистора и 2N ключа (обычно КМОП), по одному между каждым узлом цепи и выходом.

Рис. 1. Структура взвешивающего ЦАП

Взвешивающий метод — один из самых быстрых, однако характеризуется наименьшей точностью. Обычно такой ЦАП имеет выход по напряжению и отличается хорошей монотонностью. Если все резисторы одинаковы, ЦАП линеен. Недостаток данной модели — относительно высокий выходной импеданс и большое количество резисторов и ключей.

ЦАП на матрице R–2R. Это одна из наиболее распространенных структур (см. рис. 2). Здесь используются только две величины сопротивлений, находящихся в отношении 2:1. Количество резисторов равно 2N. Резистивный делитель можно использовать в качестве ЦАП двумя способами, в режиме напряжения и режиме тока (они также известны как нормальный и инверсный режимы). Главное преимущество ЦАП с выходом по напряжению заключается в том, что выходной импеданс постоянен. Второе достоинство — отсутствие емкостных токов в нагрузке. Недостатки данной структуры: во-первых, опорный источник должен иметь очень низкий импеданс; во-вторых, для регулирования усиления нельзя использовать резистор, включенный последовательно с опорным источником. В токовом режиме это допустимо, однако выбросы в токовой схеме больше. С другой стороны, ключи находятся под потенциалом земли, поэтому защита от большого перепада напряжений не требуется.

Рис. 2. ЦАП на R–2R матрице с выходом в форме напряжения

В сигма-дельта ЦАП (см. рис. 3) преобразование осуществляется с помощью сигма-дельта модуляции, когда квантование осуществляется всего одним разрядом, но с частотой, в десятки и сотни раз превышающей частоту Найквиста. Как видно из рисунка 4, сигма-дельта модулятор преобразует входной сигнал в последовательный непрерывный поток нулей и единиц. Если входной сигнал близок к положительному краю полной шкалы, в битовом потоке на выходе больше единиц, чем нулей, и наоборот, если сигнал ближе к отрицательному краю, то больше нулей. Для сигнала, близкого к середине шкалы, количество нулей и единиц примерно одинаково.

Рис. 3. Общая структура сигма-дельта ЦАП

Рис. 4. Принцип работы сигма-дельта модулятора

Интерполяционный фильтр представляет собой цифровую схему, которая принимает данные, поступающие с низкой частотой дискретизации, вставляет нули в поток данных, увеличивая тем самым частоту дискретизации, затем применяет алгоритм интерполяции и выдает данные с высокой частотой дискретизации. Выходное напряжение одноразрядного ЦАП переключается между равными по значению положительным и отрицательным опорными напряжениями. Выход фильтруется аналоговым ФНЧ.

Перемножающий ЦАП работает с различными опорными сигналами, в т.ч. переменного тока. Выходной сигнал пропорционален произведению опорного напряжения на дробный эквивалент цифрового входного числа.

Сегментированные (гибридные) преобразователи. При проектировании конкретного ЦАП может оказаться так, что ни одна из базовых структур не подходит, и придется комбинировать различные структуры для получения ЦАП с высоким разрешением и требуемыми характеристиками.

Подбор ЦАП

Для выбора подходящего ЦАП необходимо определить требования, которым должны соответствовать его параметры. В первую очередь это — разрядность, разрешение, время установления выходного сигнала (быстродействие), интерфейс подключения, напряжение питания и т.д. Обычно при проектировании устройства сначала выбирается его главный элемент — вычислительное ядро (процессор, ПЛИС, МК и т.д.), который определяет интерфейс обмена с остальными элементами схемы. В таблице 2 приведены четыре наиболее распространенных интерфейса для ЦАП.

Табл. 2. Сравнение интерфейсов ЦАП

Интерфейс	Количество выводов	Скорость работы
Параллельный	Данные: 8—16 линий; Управление и тактирование — 2—4 линии	До 100 Мбит/с
I2C	2 линии: данные и тактирование	До 1 Мбит/с
SPI	4 линии: тактовый сигнал, выходные данные, входные данные, выборка кристалла	До 400 Мбит/с
Microwire	3 линии: тактовый сигнал, входные данные, синхронизация кадра	До 400 Мбит/с

Параллельный интерфейс — наиболее простой в реализации, однако при этом используется много линий передачи данных, микросхема имеет много выводов и занимает больше места на плате. Последовательные шины I2C и SPI являются наиболее распространенными в современных МК. Недостаток SPI — его нельзя настраивать так точно, как I2C, поэтому устройства с SPI могут быть не полностью совместимы между собой.

Разрядность ЦАП и величина опорного напряжения определяют шаг изменения выходного сигнала. Время установления определяет быстродействие ЦАП. При работе с постоянными или низкочастотными сигналами этот параметр не имеет большого значения. Однако им нельзя пренебрегать при работе на ВЧ.

Нелинейности бывают двух типов: интегральная и дифференциальная. Линейный ЦАП работает как зеркало, точно отражая входные данные. Влияние нелинейностей проиллюстрировано рисунком 5. Как правило, эти искажения следует учитывать в прецизионных схемах, таких как системы калибровки или измерительное оборудование.

Рис. 5. Нелинейные искажения выходного сигнала

Для работы ЦАП нужно два источника напряжения (питания и опорное). В некоторых схемах для них используется один вывод, однако в этом случае точность ИП должна быть очень высокой, не хуже 1%. Преобразователи с раздельными выводами имеют более сложную схему, однако они не так требовательны к выбору ИП.

Тип и размер корпуса также имеют большое значение и могут существенно сузить диапазон выбора. Например, если конвейер автоматической сборки не позволяет устанавливать ИС с шариковыми выводами, то ЦАП, не выпускающиеся в других корпусах, использовать нельзя. Во-вторых, корпус может повлиять на распределение тепла на плате. В портативных устройствах и устройствах с батарейным питанием можно использовать только малопотребляющие ЦАП.

Шумовые характеристики

Источниками шума в схеме являются проводники, разъемы, трансформаторы, индуктивности, электрическое поле, создаваемое конденсаторами, антенны и прочие элементы. Наибольший вклад вносят шумы от проводящих линий.

Как известно, соединительные проводники представляют собой не только активное, но и реактивное сопротивление. Соответственно, нужно следить за тем, чтобы все контуры возвратных токов были как можно меньше, тогда индуктивность проводов уменьшается и не возникает шума по земляной шине.

Формирование выходного сигнала

ЦАП можно подключить к нагрузке напрямую, однако, как правило, ставится дополнительный буфер или согласующее устройство. Это может быть неинвертирующий ОУ или повторитель напряжения (см. рис. 6). При использовании буфера следует удостовериться, что он не вносит погрешность больше 1/2 МЗР. При согласовании ОУ с ЦАП следует учитывать и другие параметры ОУ: полосу пропускания, размах напряжения и т.д.

Рис. 6. Способы формирования выходного сигнала

Земля

Если на плате имеется только один слой земли, то шум от цифровых элементов может проникнуть в аналоговую часть схемы. Чтобы избежать этого, рекомендуется делать отдельные полигоны земли для аналоговой и цифровой частей, соединенные тонким проводником. Второй способ — использовать два внутренних слоя, соединенных сквозным отверстием. Этот метод более надежен, однако стоимость платы увеличивается.

Литература

1. McCulley В. Bridging the Divide//www.analog-europe.com/en/bridging-the-divide-part-1—dac-introduction.html?cmp_id=71&news_id=222900832&vID=35.

2. Kester W. Data Conversion Handbook//Analog Devices, 2004.

www.russianelectronics.ru

Аналого-цифровой преобразователь — Википедия

Четырёхканальный аналого-цифровой преобразователь

Аналого-цифровой преобразователь^[1]^[2]^[3] (АЦП, англ. Analog-to-digital converter, ADC) — устройство, преобразующее входной аналоговый сигнал в дискретный код (цифровой сигнал).

Обратное преобразование осуществляется при помощи цифро-аналогового преобразователя (ЦАП, DAC).

Как правило, АЦП — электронное устройство, преобразующее напряжение в двоичный цифровой код. Тем не менее, некоторые неэлектронные устройства с цифровым выходом следует также относить к АЦП, например, некоторые типы преобразователей угол-код. Простейшим одноразрядным двоичным АЦП является компаратор.

Разрешение АЦП — минимальное изменение величины аналогового сигнала, которое может быть преобразовано данным АЦП — связано с его разрядностью. В случае единичного измерения без учёта шумов разрешение напрямую определяется разрядностью АЦП.

Разрядность АЦП характеризует количество дискретных значений, которые преобразователь может выдать на выходе. В двоичных АЦП измеряется в битах, в троичных АЦП измеряется в тритах. Например, двоичный 8-разрядный АЦП способен выдать 256 дискретных значений (0…255), поскольку 28=256{\displaystyle 2^{8}=256}, троичный 8-разрядный АЦП способен выдать 6561 дискретное значение, поскольку 38=6561{\displaystyle 3^{8}=6561}.

Разрешение по напряжению равно разности напряжений, соответствующих максимальному и минимальному выходному коду, делённой на количество выходных дискретных значений. Например:

Пример 1
- Диапазон входных значений = от 0 до 10 вольт
- Разрядность двоичного АЦП 12 бит: 2¹² = 4096 уровней квантования
- Разрешение двоичного АЦП по напряжению: (10-0)/4096 = 0,00244 вольт = 2,44 мВ
- Разрядность троичного АЦП 12 трит: 3¹² = 531 441 уровень квантования
- Разрешение троичного АЦП по напряжению: (10-0)/531441 = 0,0188 мВ = 18,8 мкВ
Пример 2
- Диапазон входных значений = от −10 до +10 вольт
- Разрядность двоичного АЦП 14 бит: 2¹⁴ = 16384 уровня квантования
- Разрешение двоичного АЦП по напряжению: (10-(-10))/16384 = 20/16384 = 0,00122 вольт = 1,22 мВ
- Разрядность троичного АЦП 14 трит: 3¹⁴ = 4 782 969 уровней квантования
- Разрешение троичного АЦП по напряжению: (10-(-10))/4782969 = 0,00418 мВ = 4,18 мкВ

На практике разрешение АЦП ограничено отношением сигнал/шум входного сигнала. При большой интенсивности шумов на входе АЦП различение соседних уровней входного сигнала становится невозможным, то есть ухудшается разрешение. При этом реально достижимое разрешение описывается эффективной разрядностью (англ. effective number of bits, ENOB), которая меньше, чем реальная разрядность АЦП. При преобразовании сильно зашумлённого сигнала младшие разряды выходного кода практически бесполезны, так как содержат шум. Для достижения заявленной разрядности отношение сигнал/шум входного сигнала должно быть примерно 6 дБ на каждый бит разрядности (6 дБ соответствует двукратному изменению уровня сигнала).

По способу применяемых алгоритмов АЦП делят на:

АЦП первых двух типов подразумевают обязательное применение в своем составе устройства выборки и хранения (УВХ). Это устройство служит для запоминания аналогового значения сигнала на время, необходимое для выполнения преобразования. Без него результат преобразования АЦП последовательного типа будет недостоверным. Выпускаются интегральные АЦП последовательного приближения, как содержащие в своем составе УВХ, так и требующие внешнее УВХ^{[источник не указан 1457 дней]}.

Линейные АЦП[править | править код]

Большинство АЦП считаются линейными, хотя аналого-цифровое преобразование, по сути, является нелинейным процессом (поскольку операция отображения непрерывного пространства в дискретное — операция нелинейная).

Термин линейный применительно к АЦП означает, что диапазон входных значений, отображаемый на выходное цифровое значение, связан по линейному закону с этим выходным значением, то есть выходное значение k достигается при диапазоне входных значений от

m(k + b)

до

m(k + 1 + b),

где m и b — некоторые константы. Константа b, как правило, имеет значение 0 или −0.5. Если b = 0, АЦП называют квантователь с ненулевой ступенью (mid-rise), если же b = −0,5, то АЦП называют квантователь с нулём в центре шага квантования (mid-tread).

Нелинейные АЦП[править | править код]

Если бы плотность вероятности амплитуды входного сигнала имела равномерное распределение, то отношение сигнал/шум (применительно к шуму квантования) было бы максимально возможным. По этой причине обычно перед квантованием по амплитуде сигнал пропускают через безынерционный преобразователь, передаточная функция которого повторяет функцию распределения самого сигнала. Это улучшает достоверность передачи сигнала, так как наиболее важные области амплитуды сигнала квантуются с лучшим разрешением. Соответственно, при цифро-аналоговом преобразовании потребуется обработать сигнал функцией, обратной функции распределения исходного сигнала.

Это тот же принцип, что и используемый в компандерах, применяемых в магнитофонах и различных коммуникационных системах, он направлен на максимизацию энтропии. (Не путать компандер с компрессором!)

Например, голосовой сигнал имеет лапласово распределение амплитуды. Это означает, что окрестность нуля по амплитуде несёт больше информации, чем области с большей амплитудой. По этой причине логарифмические АЦП часто применяются в системах передачи голоса для увеличения динамического диапазона передаваемых значений без изменения качества передачи сигнала в области малых амплитуд.

8-битные логарифмические АЦП с a-законом или μ-законом обеспечивают широкий динамический диапазон и имеют высокое разрешение в наиболее критичном диапазоне малых амплитуд; линейный АЦП с подобным качеством передачи должен был бы иметь разрядность около 12 бит.

Передаточная характеристика АЦП — зависимость числового эквивалента выходного двоичного кода от величины входного аналогового сигнала. Говорят о линейных и нелинейных АЦП. Такое деление условное. Обе передаточные характеристики — ступенчатые. Но для «линейных» АЦП всегда возможно провести такую прямую линию, чтобы все точки передаточной характеристики, соответствующие входным значениям δ⋅2k{\displaystyle \delta \cdot 2^{k}} (где δ{\displaystyle \delta } — шаг дискретизации, k лежит в диапазоне 0..N, где N — разрядность АЦП), были от неё равноудалены.

Имеется несколько источников погрешности АЦП. Ошибки квантования и (считая, что АЦП должен быть линейным) нелинейности присущи любому аналого-цифровому преобразованию. Кроме того, существуют так называемые апертурные ошибки, которые являются следствием джиттера (англ. jitter) тактового генератора, они проявляются при преобразовании сигнала в целом (а не одного отсчёта).

Эти ошибки измеряются в единицах, называемых МЗР — младший значащий разряд (англ.). В приведённом выше примере 8-битного двоичного АЦП ошибка в 1 МЗР составляет 1/256 от полного диапазона сигнала, то есть 0,4 %, в 5-тритном троичном АЦП ошибка в 1 МЗР составляет 1/243 от полного диапазона сигнала, то есть 0,412 %, в 8-тритном троичном АЦП ошибка в 1 МЗР составляет 1/6561, то есть 0,015 %.

Ошибки квантования[править | править код]

Ошибки квантования являются следствием ограниченного разрешения АЦП. Этот недостаток не может быть устранён ни при каком типе аналого-цифрового преобразования. Абсолютная величина ошибки квантования при каждом отсчёте находится в пределах от нуля до половины МЗР.

Как правило, амплитуда входного сигнала много больше, чем МЗР. В этом случае ошибка квантования не коррелирована с сигналом и имеет равномерное распределение. Её среднеквадратическое значение совпадает с среднеквадратичным отклонением распределения, которое равно 112LSB≈0.289 LSB{\displaystyle {1 \over {\sqrt {12}}}\mathrm {LSB} \approx 0.289\ \mathrm {LSB} }. В случае 8-битного АЦП это составит 0,113 % от полного диапазона сигнала.

Нелинейность[править | править код]

Всем АЦП присущи ошибки, связанные с нелинейностью, которые являются следствием физического несовершенства АЦП. Это приводит к тому, что передаточная характеристика (в указанном выше смысле) отличается от линейной (точнее от желаемой функции, так как она не обязательно линейна). Ошибки могут быть уменьшены путём калибровки^[4].

Важным параметром, описывающим нелинейность, является интегральная нелинейность (INL) и дифференциальная нелинейность (DNL).

Апертурная погрешность (джиттер)[править | править код]

Пусть мы оцифровываем синусоидальный сигнал x(t)=Asin⁡2πf0t{\displaystyle x(t)=A\sin 2\pi f_{0}t}. В идеальном случае отсчёты берутся через равные промежутки времени. Однако в реальности время момента взятия отсчёта подвержено флуктуациям из-за дрожания фронта синхросигнала (clock jitter). Полагая, что неопределённость момента времени взятия отсчёта порядка Δt{\displaystyle \Delta t}, получаем, что ошибка, обусловленная этим явлением, может быть оценена как

Eap≤|x′(t)Δt|≤2Aπf0Δt{\displaystyle E_{ap}\leq |x'(t)\Delta t|\leq 2A\pi f_{0}\Delta t}.

Ошибка относительно невелика на низких частотах, однако на больших частотах она может существенно возрасти.

Эффект апертурной погрешности может быть проигнорирован, если её величина сравнительно невелика по сравнению с ошибкой квантования. Таким образом, можно установить следующие требования к дрожанию фронта сигнала синхронизации:

Δt<12qπf0{\displaystyle \Delta t<{\frac {1}{2^{q}\pi f_{0}}}},

где q{\displaystyle q} — разрядность АЦП.

Разрядность АЦП	Максимальная частота входного сигнала
Разрядность АЦП	44,1 кГц	192 кГц	1 МГц	10 МГц	100 МГц
8	28,2 нс	6,48 нс	1,24 нс	124 пс	12,4 пс
10	7,05 нс	1,62 нс	311 пс	31,1 пс	3,11 пс
12	1,76 нс	405 пс	77,7 пс	7,77 пс	777 фс
14	441 пс	101 пс	19,4 пс	1,94 пс	194 фс
16	110 пс	25,3 пс	4,86 пс	486 фс	48,6 фс
18	27,5 пс	6,32 пс	1,21 пс	121 фс	12,1 фс
24	430 фс	98,8 фс	19,0 фс	1,9 фс	190 ас

Из этой таблицы можно сделать вывод о целесообразности применения АЦП определённой разрядности с учётом ограничений, накладываемых дрожанием фронта синхронизации (clock jitter). Например, бессмысленно использовать прецизионный 24-битный АЦП для записи звука, если система распределения синхросигнала не в состоянии обеспечить ультрамалой неопределённости.

Вообще качество тактового сигнала чрезвычайно важно не только по этой причине. Например, из описания микросхемы AD9218 (Analog Devices):

Any high speed ADC is extremely sensitive to the quality of the sampling clock provided by the user. A track-and-hold circuit is essentially a mixer. Any noise, distortion, or timing jitter on the clock is combined with the desired signal at the analog-to-digital output.

То есть любой высокоскоростной АЦП крайне чувствителен к качеству оцифровывающей тактовой частоты, подаваемой пользователем. Схема выборки и хранения, по сути, является смесителем (перемножителем). Любой шум, искажения, или дрожание фазы тактовой частоты смешиваются с полезным сигналом и поступают на цифровой выход.

Аналоговый сигнал является непрерывной функцией времени, в АЦП он преобразуется в последовательность цифровых значений. Следовательно, необходимо определить частоту выборки цифровых значений из аналогового сигнала. Частота, с которой производятся цифровые значения, получила название частота дискретизации АЦП.

Непрерывно меняющийся сигнал с ограниченной спектральной полосой подвергается оцифровке (то есть значения сигнала измеряются через интервал времени T — период дискретизации), и исходный сигнал может быть точно восстановлен из дискретных во времени значений путём интерполяции. Точность восстановления ограничена ошибкой квантования. Однако в соответствии с теоремой Котельникова — Шеннона точное восстановление возможно, только если частота дискретизации выше, чем удвоенная максимальная частота в спектре сигнала.

Поскольку реальные АЦП не могут произвести аналого-цифровое преобразование мгновенно, входное аналоговое значение должно удерживаться постоянным, по крайней мере, от начала до конца процесса преобразования (этот интервал времени называют время преобразования). Эта задача решается путём использования специальной схемы на входе АЦП — устройства выборки-хранения (УВХ). УВХ, как правило, хранит входное напряжение на конденсаторе, который соединён со входом через аналоговый ключ: при замыкании ключа происходит выборка входного сигнала (конденсатор заряжается до входного напряжения), при размыкании — хранение. Многие АЦП, выполненные в виде интегральных микросхем, содержат встроенное УВХ.

Все АЦП работают путём выборки входных значений через фиксированные интервалы времени. Следовательно, выходные значения являются неполной картиной того, что подаётся на вход. Глядя на выходные значения, нет никакой возможности установить, как вёл себя входной сигнал между выборками. Если известно, что входной сигнал меняется достаточно медленно относительно частоты дискретизации, то можно предположить, что промежуточные значения между выборками находятся где-то между значениями этих выборок. Если же входной сигнал меняется быстро, то никаких предположений о промежуточных значениях входного сигнала сделать нельзя, а следовательно, невозможно однозначно восстановить форму исходного сигнала.

Если последовательность цифровых значений, выдаваемая АЦП, где-либо преобразуется обратно в аналоговую форму цифро-аналоговым преобразователем, желательно, чтобы полученный аналоговый сигнал был максимально точной копией исходного сигнала. Если входной сигнал меняется быстрее, чем делаются его отсчёты, то точное восстановление сигнала невозможно, и на выходе ЦАП будет присутствовать ложный сигнал. Ложные частотные компоненты сигнала (отсутствующие в спектре исходного сигнала) получили название alias (ложная частота, побочная низкочастотная составляющая). Частота ложных компонент зависит от разницы между частотой сигнала и частотой дискретизации. Например, синусоидальный сигнал с частотой 2 кГц, дискретизованный с частотой 1.5 кГц, был бы воспроизведён как синусоида с частотой 500 Гц. Эта проблема получила название наложение частот (aliasing).

Для предотвращения наложения спектров сигнал, подаваемый на вход АЦП, должен быть пропущен через фильтр нижних частот для подавления спектральных компонент, частота которых превышает половину частоты дискретизации. Этот фильтр получил название anti-aliasing (антиалиасинговый) фильтр, его применение чрезвычайно важно при построении реальных АЦП.

Вообще, применение аналогового входного фильтра интересно не только по этой причине. Казалось бы, цифровой фильтр, который обычно применяется после оцифровки, имеет несравненно лучшие параметры. Но, если в сигнале присутствуют компоненты, значительно более мощные, чем полезный сигнал, и достаточно далеко отстоящие от него по частоте, чтобы быть эффективно подавленными аналоговым фильтром, такое решение позволяет сохранить динамический диапазон АЦП: если помеха на 10 дБ сильнее сигнала, на неё впустую будет тратиться, в среднем, три бита разрядности.

Хотя наложение спектров в большинстве случаев является нежелательным эффектом, его можно использовать во благо. Например, благодаря этому эффекту можно обойтись без преобразования частоты вниз при оцифровке узкополосного высокочастотного сигнала (смотрите смеситель). Для этого, однако, входные аналоговые каскады АЦП должны иметь значительно более высокие параметры, чем это требуется для стандартного использования АЦП на основной (видео или низшей) гармонике. Также для этого необходимо обеспечить эффективную фильтрацию внеполосных частот до АЦП, так как после оцифровки нет никакой возможности идентифицировать и/или отфильтровать большинство из них.

Некоторые характеристики АЦП могут быть улучшены путём использования методики подмешивания псевдослучайного сигнала (англ. dither). Она заключается в добавлении к входному аналоговому сигналу случайного шума (белый шум) небольшой амплитуды. Амплитуда шума, как правило, выбирается на уровне половины МЗР. Эффект от такого добавления заключается в том, что состояние МЗР случайным образом переходит между состояниями 0 и 1 при очень малом входном сигнале (без добавления шума МЗР был бы в состоянии 0 или 1 долговременно). Для сигнала с подмешанным шумом вместо простого округления сигнала до ближайшего разряда происходит случайное округление вверх или вниз, причём среднее время, в течение которого сигнал округлён к тому или иному уровню, зависит от того, насколько сигнал близок к этому уровню. Таким образом, оцифрованный сигнал содержит информацию об амплитуде сигнала с разрешающей способностью лучше, чем МЗР, то есть происходит увеличение эффективной разрядности АЦП. Негативной стороной методики является увеличение шума в выходном сигнале. Фактически ошибка квантования размазывается по нескольким соседним отсчётам. Такой подход является более желательным, чем простое округление до ближайшего дискретного уровня. В результате использования методики подмешивания псевдослучайного сигнала мы имеем более точное воспроизведение сигнала во времени. Малые изменения сигнала могут быть восстановлены из псевдослучайных скачков МЗР путём фильтрации. Кроме того, если шум детерминирован (амплитуда добавляемого шума точно известна в любой момент времени), то его можно вычесть из оцифрованного сигнала, предварительно увеличив его разрядность, тем самым почти полностью избавиться от добавленного шума.

Звуковые сигналы очень малых амплитуд, оцифрованные без псевдослучайного сигнала, воспринимаются на слух очень искажёнными и неприятными. При подмешивании псевдослучайного сигнала истинный уровень сигнала представлен средним значением нескольких последовательных отсчётов.

Однако с 2009 года, в связи с удешевлением 24-битных АЦП, имеющих даже без dither’а динамический диапазон более 120 дБ, что на несколько порядков превышает полный воспринимаемый человеком диапазон слуха, данная технология потеряла актуальность в звукотехнике. При этом она используется в ВЧ- и СВЧ-технике, где битность АЦП обычно мала из-за высокой частоты дискретизации.

Похожий процесс, также называемый dither или диффузия ошибок, применяется для представления полутонов изображений в компьютерной графике при малом количестве бит на пиксел. При этом изображение становится зашумлённым, но визуально воспринимается реалистичнее, чем то же изображение, полученное простым квантованием.

Как правило, сигналы оцифровываются с минимально необходимой частотой дискретизации из соображений экономии, при этом шум квантования является белым, то есть его спектральная плотность мощности равномерно распределена во всей полосе. Если же оцифровать сигнал с частотой дискретизации, гораздо большей, чем по теореме Котельникова — Шеннона, а затем подвергнуть цифровой фильтрации для подавления спектра вне частотной полосы исходного сигнала, то отношение сигнал/шум будет лучше, чем при использовании всей полосы. Таким образом можно достичь эффективного разрешения большего, чем разрядность АЦП.

Передискретизация также может быть использована для смягчения требований к крутизне перехода от полосы пропускания к полосе подавления антиалиасингового фильтра. Для этого сигнал оцифровывают, например, на вдвое большей частоте, затем производят цифровую фильтрацию, подавляя частотные компоненты вне полосы исходного сигнала, и, наконец, понижают частоту дискретизации путём децимации.

Ниже перечислены основные способы построения электронных АЦП:

АЦП прямого преобразования[править | править код]

Параллельные АЦП прямого преобразования (Direct-conversion (Flash) ADC), полностью параллельные АЦП, содержат по одному компаратору на каждый дискретный уровень входного сигнала. В любой момент времени только компараторы, соответствующие уровням ниже уровня входного сигнала, выдают на своём выходе сигнал превышения. Сигналы со всех компараторов поступают либо прямо в параллельный регистр, тогда обработка кода осуществляется программно, либо на аппаратный логический шифратор, аппаратно генерирующий нужный цифровой код в зависимости от кода на входе шифратора. Данные с шифратора фиксируются в параллельном регистре. Частота дискретизации параллельных АЦП, в общем случае, зависит от аппаратных характеристик аналоговых и логических элементов, а также от требуемой частоты выборки значений. Параллельные АЦП прямого преобразования — самые быстрые, но обычно имеют разрешение от 8 бит, как цифровые осциллографы, так как влекут за собой большие аппаратные затраты (2n−1=28−1=255{\displaystyle 2^{n}-1=2^{8}-1=255} компараторов). АЦП этого типа имеют очень большой размер кристалла микросхемы, высокую входную ёмкость, и могут выдавать кратковременные ошибки на выходе. Часто используются для видео или других высокочастотных сигналов, а также широко применяются в промышленности для отслеживания быстро изменяющихся процессов в реальном времени. Профессиональные модели могут иметь разрешение до 14 бит и выше^[5].
Параллельно-последовательные АЦП прямого преобразования (Subranging Direct-conversion (Flash) ADC)^[6] частично последовательные АЦП. Были предложены R. Staffin и R. Lohman R. в 1956 году (Staffin and R. Lohman, «Signal Amplitude Quantizer», U.S. Patent 2,869,079, Filed December 19, 1956, Issued January 13, 1959)^[7]. Немного уменьшая быстродействие позволяют значительно уменьшить количество ОУ до k⋅(2n/k−1)+k−1{\displaystyle k\cdot (2^{n/k}-1)+k-1}, где n — число битов выходного кода, а k — число параллельных АЦП прямого преобразования. При 8 битах и 2 АЦП потребуется 31 ОУ. Используют два (k=2) или более шагов-поддиапазонов. При k=2 преобразователь называется Half-Flash (Subranging) ADC. Второй, третий и т. д. АЦП служат для уменьшения ошибки квантования первого АЦП путём оцифровки этой ошибки. На первом шаге производится грубое преобразование (с низким разрешением). Далее определяется разница между входным сигналом и аналоговым сигналом, соответствующим результату грубого преобразования (со вспомогательного ЦАП, на который подаётся грубый код). На втором шаге найденная разница умножается на 2n/k{\displaystyle 2^{n/k}} и подвергается следующему преобразованию. Полученный код объединяется с грубым кодом для получения полного выходного цифрового значения. АЦП этого типа медленнее параллельных АЦП прямого преобразования, имеют высокое разрешение и небольшой размер корпуса. Для увеличения скорости выходного оцифрованного потока данных в параллельно-последовательных АЦП прямого преобразования применяется конвейерная работа параллельных АЦП.
Конвейерная работа АЦП (Pipelined Subranging Direct-conversion (Flash) ADC)^[8], применяется в параллельно-последовательных АЦП прямого преобразования, в отличие от обычного режима работы параллельно-последовательных АЦП прямого преобразования, в котором данные передаются после полного преобразования, при конвейерной работе данные частичных преобразований передаются по мере готовности до окончания полного преобразования. В 1966 году Kinniment и др. предложили архитектуру параллельно-последовательного АЦП прямого преобразования с рециркуляцией (Recirculating ADC Architecture)^[9]. В этой архитектуре используется один поддиапазонный параллельный АЦП прямого преобразования.
Последовательные АЦП прямого преобразования (Subranging Direct-conversion (Flash) ADC), полностью последовательные АЦП (k=n), медленнее параллельных АЦП прямого преобразования и немного медленнее параллельно-последовательных АЦП прямого преобразования, но ещё больше (до n⋅(2n/n−1)+n−1=n⋅(21−1)+n−1=2n−1{\displaystyle n\cdot (2^{n/n}-1)+n-1=n\cdot (2^{1}-1)+n-1=2n-1}, где n — число битов выходного кода, а k — число параллельных АЦП прямого преобразования) уменьшают количество ОУ (при 8 битах потребуется 15 ОУ: 8 компараторов на ОУ и 7 вычитателей-умножителей на 2 на ОУ)^[10]. Троичные АЦП этого вида приблизительно в 1,5 раза быстрее соизмеримых по числу уровней и аппаратных затрат двоичных АЦП этого же вида^[11].

АЦП последовательного приближения[править | править код]

АЦП последовательного приближения или АЦП с поразрядным уравновешиванием содержит компаратор, вспомогательный ЦАП и регистр последовательного приближения. АЦП преобразует аналоговый сигнал в цифровой за N шагов, где N — разрядность АЦП. На каждом шаге определяется по одному биту искомого цифрового значения, начиная от СЗР (Старшего Значащего Разряда) и заканчивая МЗР (Младшим Значащим Разрядом). Последовательность действий по определению очередного бита заключается в следующем. На вспомогательном ЦАП выставляется аналоговое значение, образованное из битов, уже определённых на предыдущих шагах; бит, который должен быть определён на этом шаге, выставляется в 1, более младшие биты установлены в 0. Полученное на вспомогательном ЦАП значение сравнивается с входным аналоговым значением. Если значение входного сигнала больше значения на вспомогательном ЦАП, то определяемый бит получает значение 1, в противном случае 0. Таким образом, определение итогового цифрового значения напоминает двоичный поиск. АЦП этого типа обладают одновременно высокой скоростью и хорошим разрешением. Однако при отсутствии устройства выборки хранения погрешность будет значительно больше (представьте, что после оцифровки самого большого разряда сигнал начал меняться).

АЦП дифференциального кодирования[править | править код]

АЦП дифференциального кодирования (англ. delta-encoded ADC) содержат реверсивный счётчик, код с которого поступает на вспомогательный ЦАП. Входной сигнал и сигнал со вспомогательного ЦАП сравниваются на компараторе. Благодаря отрицательной обратной связи с компаратора на счётчик код на счётчике постоянно меняется так, чтобы сигнал со вспомогательного ЦАП как можно меньше отличался от входного сигнала. По прошествии некоторого времени разница сигналов становится меньше, чем МЗР, при этом код счётчика считывается как выходной цифровой сигнал АЦП. АЦП этого типа имеют очень большой диапазон входного сигнала и высокое разрешение, но время преобразования зависит от входного сигнала, хотя и ограничено сверху. В худшем случае время преобразования равно T_max=(2^q)/f_с, где q — разрядность АЦП, f_с — частота тактового генератора счётчика. АЦП дифференциального кодирования обычно являются хорошим выбором для оцифровки сигналов реального мира, так как большинство сигналов в физических системах не склонны к скачкообразным изменениям. В некоторых АЦП применяется комбинированный подход: дифференциальное кодирование и последовательное приближение; это особенно хорошо работает в случаях, когда известно, что высокочастотные компоненты в сигнале относительно невелики.

АЦП сравнения с пилообразным сигналом[править | править код]

АЦП сравнения с пилообразным сигналом (некоторые АЦП этого типа называют Интегрирующие АЦП, также к ним относятся АЦП последовательного счета) содержат генератор пилообразного напряжения (в АЦП последовательного счета генератор ступенчатого напряжения, состоящий из счетчика и ЦАП), компаратор и счётчик времени. Пилообразный сигнал линейно нарастает от нижнего до верхнего уровня, затем быстро спадает до нижнего уровня. В момент начала нарастания запускается счётчик времени. Когда пилообразный сигнал достигает уровня входного сигнала, компаратор срабатывает и останавливает счётчик; значение считывается со счётчика и подаётся на выход АЦП. Данный тип АЦП является наиболее простым по структуре и содержит минимальное число элементов. Вместе с тем простейшие АЦП этого типа обладают довольно низкой точностью и чувствительны к температуре и другим внешним параметрам. Для увеличения точности генератор пилообразного сигнала может быть построен на основе счётчика и вспомогательного ЦАП, однако такая структура не имеет никаких других преимуществ по сравнению с АЦП последовательного приближения и АЦП дифференциального кодирования.

АЦП с уравновешиванием заряда[править | править код]

АЦП с уравновешиванием заряда (к ним относятся АЦП с двухстадийным интегрированием, АЦП с многостадийным интегрированием и некоторые другие) содержат генератор стабильного тока, компаратор, интегратор тока, тактовый генератор и счётчик импульсов. Преобразование происходит в два этапа (двухстадийное интегрирование). На первом этапе значение входного напряжения преобразуется в ток (пропорциональный входному напряжению), который подаётся на интегратор тока, заряд которого изначально равен нулю. Этот процесс длится в течение времени TN, где T — период тактового генератора, N — константа (большое целое число, определяет время накопления заряда). По прошествии этого времени вход интегратора отключается от входа АЦП и подключается к генератору стабильного тока. Полярность генератора такова, что он уменьшает заряд, накопленный в интеграторе. Процесс разряда длится до тех пор, пока заряд в интеграторе не уменьшится до нуля. Время разряда измеряется путём счёта тактовых импульсов от момента начала разряда до достижения нулевого заряда на интеграторе. Посчитанное количество тактовых импульсов и будет выходным кодом АЦП. Можно показать, что количество импульсов n, посчитанное за время разряда, равно: n=U_вхN(RI₀)⁻¹, где U_вх — входное напряжение АЦП, N — число импульсов этапа накопления (определено выше), R — сопротивление резистора, преобразующего входное напряжение в ток, I₀ — значение тока от генератора стабильного тока, разряжающего интегратор на втором этапе. Таким образом, потенциально нестабильные параметры системы (прежде всего, ёмкость конденсатора интегратора) не входят в итоговое выражение. Это является следствием двухстадийности процесса: погрешности, введённые на первом и втором этапах, взаимно вычитаются. Не предъявляются жёсткие требования даже к долговременной стабильности тактового генератора и напряжению смещения компаратора: эти параметры должны быть стабильны лишь кратковременно, то есть в течение каждого преобразования (не более 2TN). Фактически принцип двухстадийного интегрирования позволяет напрямую преобразовывать отношение двух аналоговых величин (входного и образцового тока) в отношение числовых кодов (n и N в терминах, определённых выше) практически без внесения дополнительных ошибок. Типичная разрядность АЦП этого типа составляет от 10 до 18^{[источник не указан 2236 дней]} двоичных разрядов. Дополнительным достоинством является возможность построения преобразов

ru.wikipedia.org

Принцип работы цифро – аналогового преобразователя

В процессе управления каким – то объектом необходимо следить за его состоянием. То есть следить за напряжением, током устройства а также различными не электрическими величинами, например скорость, перемещение, температура и так далее. В процессе обработки данных нам необходимо переводить физические величины в цифровой код, а также цифровой код переводить в физические величины. Для этого существуют такие устройства как аналого – цифровой преобразователь (АЦП) – который переводит физическую величину в код и цифро – аналоговый преобразователь (ЦАП) – он выполняет обратное действие АЦП. В данной статье мы рассмотрим цифро – аналоговый преобразователь (ЦАП).

Структурная схема преобразователя числа в напряжение реализованного на операционном усилителе показана ниже:

Здесь правая часть схемы представляет собой обычный сумматор с четырьмя входами. При подаче к входам напряжений U₁, U₂, U₃, U₄получим на выходе:

Условимся что сопротивления резисторов соответствуют соотношениям , , , , тогда :

Допустим что выходные напряжения равны один вольт, и с помощью четырех логических элементов обеспечим их появление только при условии, что будет подан сигнал из регистра в соответствии с числом. Если мы произведем запись в регистр числа 5, что равно 0101, то U₁=0, U₂=1, U₃=0, U₄=1. Из приведенного выше уравнения видно, что выходное напряжение будет равно U_вых=4+1= 5 В. На выходе ЦАП появится аналоговый сигнал, который будет соответствовать числу, которое записано в регистр.

elenergi.ru

Аналого-цифровое преобразование для начинающих / Habr

В этой статье рассмотрены основные вопросы, касающиеся принципа действия АЦП различных типов. При этом некоторые важные теоретические выкладки, касающиеся математического описания аналого-цифрового преобразования остались за рамками статьи, но приведены ссылки, по которым заинтересованный читатель сможет найти более глубокое рассмотрение теоретических аспектов работы АЦП. Таким образом, статья касается в большей степени понимания общих принципов функционирования АЦП, чем теоретического анализа их работы.

Введение

В качестве отправной точки дадим определение аналого-цифровому преобразованию. Аналого-цифровое преобразование – это процесс преобразования входной физической величины в ее числовое представление. Аналого-цифровой преобразователь – устройство, выполняющее такое преобразование. Формально, входной величиной АЦП может быть любая физическая величина – напряжение, ток, сопротивление, емкость, частота следования импульсов, угол поворота вала и т.п. Однако, для определенности, в дальнейшем под АЦП мы будем понимать исключительно преобразователи напряжение-код.

Понятие аналого-цифрового преобразования тесно связано с понятием измерения. Под измерением понимается процесс сравнения измеряемой величины с некоторым эталоном, при аналого-цифровом преобразовании происходит сравнение входной величины с некоторой опорной величиной (как правило, с опорным напряжением). Таким образом, аналого-цифровое преобразование может рассматриваться как измерение значения входного сигнала, и к нему применимы все понятия метрологии, такие, как погрешности измерения.

Основные характеристики АЦП

АЦП имеет множество характеристик, из которых основными можно назвать частоту преобразования и разрядность. Частота преобразования обычно выражается в отсчетах в секунду (samples per second, SPS), разрядность – в битах. Современные АЦП могут иметь разрядность до 24 бит и скорость преобразования до единиц GSPS (конечно, не одновременно). Чем выше скорость и разрядность, тем труднее получить требуемые характеристики, тем дороже и сложнее преобразователь. Скорость преобразования и разрядность связаны друг с другом определенным образом, и мы можем повысить эффективную разрядность преобразования, пожертвовав скоростью.

Типы АЦП

Существует множество типов АЦП, однако в рамках данной статьи мы ограничимся рассмотрением только следующих типов:

АЦП параллельного преобразования (прямого преобразования, flash ADC)
АЦП последовательного приближения (SAR ADC)
дельта-сигма АЦП (АЦП с балансировкой заряда)

Существуют также и другие типы АЦП, в том числе конвейерные и комбинированные типы, состоящие из нескольких АЦП с (в общем случае) различной архитектурой. Однако приведенные выше архитектуры АЦП являются наиболее показательными в силу того, что каждая архитектура занимает определенную нишу в общем диапазоне скорость-разрядность.

Наибольшим быстродействием и самой низкой разрядностью обладают АЦП прямого (параллельного) преобразования. Например, АЦП параллельного преобразования TLC5540 фирмы Texas Instruments обладает быстродействием 40MSPS при разрядности всего 8 бит. АЦП данного типа могут иметь скорость преобразования до 1 GSPS. Здесь можно отметить, что еще большим быстродействием обладают конвейерные АЦП (pipelined ADC), однако они являются комбинацией нескольких АЦП с меньшим быстродействием и их рассмотрение выходит за рамки данной статьи.

Среднюю нишу в ряду разрядность-скорость занимают АЦП последовательного приближения. Типичными значениями является разрядность 12-18 бит при частоте преобразования 100KSPS-1MSPS.

Наибольшей точности достигают сигма-дельта АЦП, имеющие разрядность до 24 бит включительно и скорость от единиц SPS до единиц KSPS.

Еще одним типом АЦП, который находил применение в недавнем прошлом, является интегрирующий АЦП. Интегрирующие АЦП в настоящее время практически полностью вытеснены другими типами АЦП, но могут встретиться в старых измерительных приборах.

АЦП прямого преобразования

АЦП прямого преобразования получили широкое распространение в 1960-1970 годах, и стали производиться в виде интегральных схем в 1980-х. Они часто используются в составе «конвейерных» АЦП (в данной статье не рассматриваются), и имеют разрядность 6-8 бит при скорости до 1 GSPS.

Архитектура АЦП прямого преобразования изображена на рис. 1

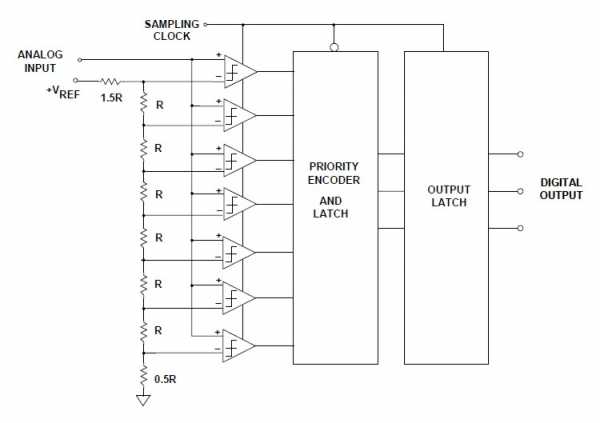
Рис. 1. Структурная схема АЦП прямого преобразования

Принцип действия АЦП предельно прост: входной сигнал поступает одновременно на все «плюсовые» входы компараторов, а на «минусовые» подается ряд напряжений, получаемых из опорного путем деления резисторами R. Для схемы на рис. 1 этот ряд будет таким: (1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16) Uref, где Uref – опорное напряжение АЦП.

Пусть на вход АЦП подается напряжение, равное 1/2 Uref. Тогда сработают первые 4 компаратора (если считать снизу), и на их выходах появятся логические единицы. Приоритетный шифратор (priority encoder) сформирует из «столбца» единиц двоичный код, который фиксируется выходным регистром.

Теперь становятся понятны достоинства и недостатки такого преобразователя. Все компараторы работают параллельно, время задержки схемы равно времени задержки в одном компараторе плюс время задержки в шифраторе. Компаратор и шифратор можно сделать очень быстрыми, в итоге вся схема имеет очень высокое быстродействие.

Но для получения N разрядов нужно 2^N компараторов (и сложность шифратора тоже растет как 2^N). Схема на рис. 1. содержит 8 компараторов и имеет 3 разряда, для получения 8 разрядов нужно уже 256 компараторов, для 10 разрядов – 1024 компаратора, для 24-битного АЦП их понадобилось бы свыше 16 млн. Однако таких высот техника еще не достигла.

АЦП последовательного приближения

АЦП последовательного приближения реализует алгоритм «взвешивания», восходящий еще к Фибоначчи. В своей книге «Liber Abaci» (1202 г.) Фибоначчи рассмотрел «задачу о выборе наилучшей системы гирь», то есть о нахождении такого ряда весов гирь, который бы требовал для нахождения веса предмета минимального количества взвешиваний на рычажных весах. Решением этой задачи является «двоичный» набор гирь. Подробнее о задаче Фибоначчи можно прочитать, например, здесь: http://www.goldenmuseum.com/2015AMT_rus.html.

Аналого-цифровой преобразователь последовательного приближения (SAR, Successive Approximation Register) измеряет величину входного сигнала, осуществляя ряд последовательных «взвешиваний», то есть сравнений величины входного напряжения с рядом величин, генерируемых следующим образом:

1. на первом шаге на выходе встроенного цифро-аналогового преобразователя устанавливается величина, равная 1/2Uref (здесь и далее мы предполагаем, что сигнал находится в интервале (0 – Uref).

2. если сигнал больше этой величины, то он сравнивается с напряжением, лежащим посередине оставшегося интервала, т.е., в данном случае, 3/4Uref. Если сигнал меньше установленного уровня, то следующее сравнение будет производиться с меньшей половиной оставшегося интервала (т.е. с уровнем 1/4Uref).

3. Шаг 2 повторяется N раз. Таким образом, N сравнений («взвешиваний») порождает N бит результата.

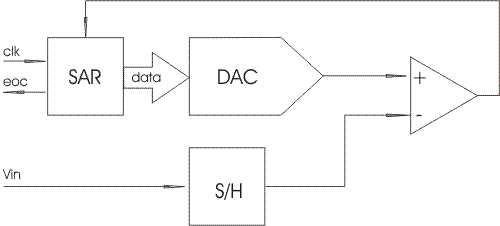
Рис. 2. Структурная схема АЦП последовательного приближения.

Таким образом, АЦП последовательного приближения состоит из следующих узлов:

1. Компаратор. Он сравнивает входную величину и текущее значение «весового» напряжения (на рис. 2. обозначен треугольником).

2. Цифро-аналоговый преобразователь (Digital to Analog Converter, DAC). Он генерирует «весовое» значение напряжения на основе поступающего на вход цифрового кода.

3. Регистр последовательного приближения (Successive Approximation Register, SAR). Он осуществляет алгоритм последовательного приближения, генерируя текущее значение кода, подающегося на вход ЦАП. По его названию названа вся данная архитектура АЦП.

4. Схема выборки-хранения (Sample/Hold, S/H). Для работы данного АЦП принципиально важно, чтобы входное напряжение сохраняло неизменную величину в течение всего цикла преобразования. Однако «реальные» сигналы имеют свойство изменяться во времени. Схема выборки-хранения «запоминает» текущее значение аналогового сигнала, и сохраняет его неизменным на протяжении всего цикла работы устройства.

Достоинством устройства является относительно высокая скорость преобразования: время преобразования N-битного АЦП составляет N тактов. Точность преобразования ограничена точностью внутреннего ЦАП и может составлять 16-18 бит (сейчас стали появляться и 24-битные SAR ADC, например, AD7766 и AD7767).

Дельта-сигма АЦП

И, наконец, самый интересный тип АЦП – сигма-дельта АЦП, иногда называемый в литературе АЦП с балансировкой заряда. Структурная схема сигма-дельта АЦП приведена на рис. 3.

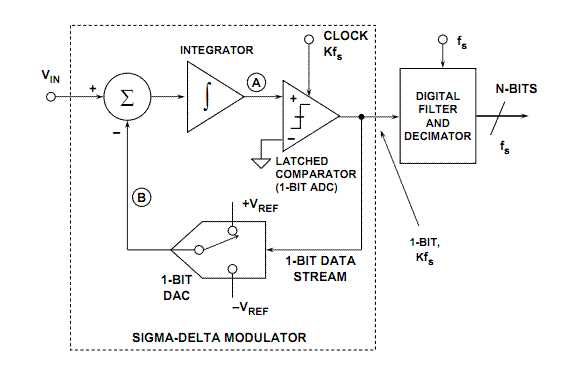
Рис.3. Структурная схема сигма-дельта АЦП.

Принцип действия данного АЦП несколько более сложен, чем у других типов АЦП. Его суть в том, что входное напряжение сравнивается со значением напряжения, накопленным интегратором. На вход интегратора подаются импульсы положительной или отрицательной полярности, в зависимости от результата сравнения. Таким образом, данный АЦП представляет собой простую следящую систему: напряжение на выходе интегратора «отслеживает» входное напряжение (рис. 4). Результатом работы данной схемы является поток нулей и единиц на выходе компаратора, который затем пропускается через цифровой ФНЧ, в результате получается N-битный результат. ФНЧ на рис. 3. Объединен с «дециматором», устройством, снижающим частоту следования отсчетов путем их «прореживания».

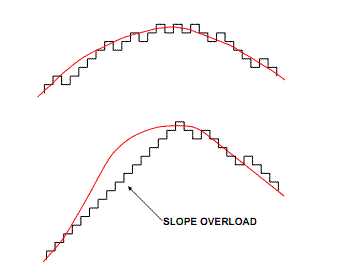
Рис. 4. Сигма-дельта АЦП как следящая система

Ради строгости изложения, нужно сказать, что на рис. 3 изображена структурная схема сигма-дельта АЦП первого порядка. Сигма-дельта АЦП второго порядка имеет два интегратора и две петли обратной связи, но здесь рассматриваться не будет. Интересующиеся данной темой могут обратиться к [3].

На рис. 5 показаны сигналы в АЦП при нулевом уровне на входе (сверху) и при уровне Vref/2 (снизу).

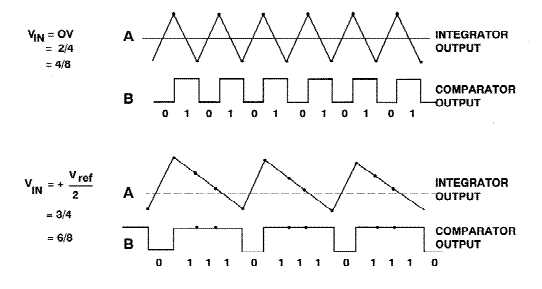
Рис. 5. Сигналы в АЦП при разных уровнях сигнала на входе.

Более наглядно работу сигма-дельта АЦП демонстрирует небольшая программа, находящаяся тут: http://designtools.analog.com/dt/sdtutorial/sdtutorial.html.

Теперь, не углубляясь в сложный математический анализ, попробуем понять, почему сигма-дельта АЦП обладают очень низким уровнем собственных шумов.

Рассмотрим структурную схему сигма-дельта модулятора, изображенную на рис. 3, и представим ее в таком виде (рис. 6):

Рис. 6. Структурная схема сигма-дельта модулятора

Здесь компаратор представлен как сумматор, который суммирует непрерывный полезный сигнал и шум квантования.

Пусть интегратор имеет передаточную функцию 1/s. Тогда, представив полезный сигнал как X(s), выход сигма-дельта модулятора как Y(s), а шум квантования как E(s), получаем передаточную функцию АЦП:

Y(s) = X(s)/(s+1) + E(s)s/(s+1)

То есть, фактически сигма-дельта модулятор является фильтром низких частот (1/(s+1)) для полезного сигнала, и фильтром высоких частот (s/(s+1)) для шума, причем оба фильтра имеют одинаковую частоту среза. Шум, сосредоточенный в высокочастотной области спектра, легко удаляется цифровым ФНЧ, который стоит после модулятора.

Рис. 7. Явление «вытеснения» шума в высокочастотную часть спектра

Однако следует понимать, что это чрезвычайно упрощенное объяснение явления вытеснения шума (noise shaping) в сигма-дельта АЦП.

Итак, основным достоинством сигма-дельта АЦП является высокая точность, обусловленная крайне низким уровнем собственного шума. Однако для достижения высокой точности нужно, чтобы частота среза цифрового фильтра была как можно ниже, во много раз меньше частоты работы сигма-дельта модулятора. Поэтому сигма-дельта АЦП имеют низкую скорость преобразования.

Они могут использоваться в аудиотехнике, однако основное применение находят в промышленной автоматике для преобразования сигналов датчиков, в измерительных приборах, и в других приложениях, где требуется высокая точность. но не требуется высокой скорости.

Немного истории

Самым старым упоминанием АЦП в истории является, вероятно, патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Изображенное в патенте устройство фактически является 5-битным АЦП прямого преобразования.

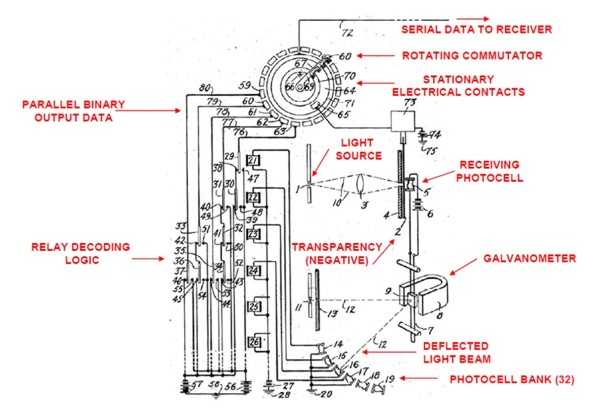
Рис. 8. Первый патент на АЦП

Рис. 9. АЦП прямого преобразования (1975 г.)

Устройство, изображенное на рисунке, представляет собой АЦП прямого преобразования MOD-4100 производства Computer Labs, 1975 года выпуска, собранный на основе дискретных компараторов. Компараторов 16 штук (они расположены полукругом, для того, чтобы уравнять задержку распространения сигнала до каждого компаратора), следовательно, АЦП имеет разрядность всего 4 бита. Скорость преобразования 100 MSPS, потребляемая мощность 14 ватт.

На следующем рисунке изображена продвинутая версия АЦП прямого преобразования.

Рис. 10. АЦП прямого преобразования (1970 г.)

Устройство VHS-630 1970 года выпуска, произведенное фирмой Computer Labs, содержало 64 компаратора, имело разрядность 6 бит, скорость 30MSPS и потребляло 100 ватт (версия 1975 года VHS-675 имела скорость 75 MSPS и потребление 130 ватт).

Литература

W. Kester. ADC Architectures I: The Flash Converter. Analog Devices, MT-020 Tutorial. www.analog.com/static/imported-files/tutorials/MT-020.pdf
W. Kester. ADC Architectures II: Successive Approximation ADC. Analog Devices, MT-021 Tutorial. www.analog.com/static/imported-files/tutorials/MT-021.pdf
W. Kester. ADC Architectures III: Sigma-Delta ADC Basics. Analog Devices, MT-022 Tutorial. www.analog.com/static/imported-files/tutorials/MT-022.pdf
W. Kester. ADC Architectures IV: Sigma-Delta ADC Advanced Concepts and Applications. Analog Devices, MT-023 Tutorial. www.analog.com/static/imported-files/tutorials/MT-023.pdf

habr.com

Процессоры (ЦАП-DAC)

Возможность модернизации для воспроизведения форматов Super Audio CD или 24-бит/96кГц.
Модульность конструкции некоторых цифровых процессоров позволяет относительно легко приспособить их для воспроизведения одного из новых высокоразрешающих цифровых форматов звука.

Как работает ЦАП (DAC)

Приводимая здесь информация адресована тем, кто хочет понять, что происходит внутри этих металлических «монументов» на стойке с вашей аппаратурой. Главные компоненты процессора: источник питания, входной приемник, цифровой фильтр, каскад цифро-аналогового преобразования, преобразователь тока в напряжение и аналоговый выходной каскад.

Входной приемник получает S/PDIF-сигнал от цифрового источника и преобразует последовательный поток данных в необработанные данные цифрового звука. Он также вырабатывает тактовый сигнал по тактовым импульсам, имеющимся в цифровом потоке (более подробно это описано в данной главе ниже). Схема фазовой автоподстройки частоты (ФАПЧ) сравнивает частоту входного сигнала (тактовые импульсы) с опорной частотой (обычно вырабатываемой кварцевым генератором) и создает новый тактовый сигнал, синхронизированный по фазе с тактовыми импульсами входного потока данных. Эти так называемые «восстановленные» тактовые импульсы становятся задающим тактовым сигналом для процессора. Входной приемник является основным источником джиттера в тактовом сигнале и может оказывать большое влияние на то, как звучит процессор. Для минимизации джиттера, создаваемого входным приемником, в последнее время используют двойные системы ФАПЧ и заказные модули с низким значением джиттера. Цифровые данные с входного приемника поступают на цифровой фильтр.

Для того, чтобы подавить паразитные спектры сигнала с центральными частотами, кратными частоте дискретизации, требуется фильтр. Фильтр может создать новые отсчеты сигнала, расположенные между исходными отсчетами звука, увеличивая таким образом частоту дискретизации. Этот процесс, называемый передискретизацией, увеличивает действующую частоту дискретизации с 44.1 кГц до кратной величины. Например, цифровой фильтр с восьмикратной передискретизацией может путем интерполяции вычислить семь новых отсчетов для каждого исходного отсчета, давая частоту дискретизации 352,8 кГц (8×44,1 кГц). Паразитные спектры по-прежнему имеются, но теперь они далеко отодвинуты от диапазона звуковых частот.

У производителей CD-проигрывателей и цифровых процессоров есть два варианта выбора: купить готовую микросхему фильтра, выполняющего восьмикратную (8х) передискретизацию, или создать нестандартный фильтр на основе универсальной микросхемы цифрового сигнального процессора (DSP). Разработчик такого фильтра должен написать программу, которая управляет микросхемой DSP, что дорого и требует времени. Следовательно, нестандартные фильтры намного дороже, но они дают разработчику CD-проигрывателя возможность творчески управлять звучанием аппарата. К тому же нестандартные цифровые фильтры могут работать быстрее, чем однокристальные фильтры с восьмикратной передискретизацией. Нестандартный фильтр можно сделать для работы с 16-, 32- и даже 64-кратной передискретизацией. Сторонники этого решения — особенно фирмы «Кгеll», «Theta» и «Wadia» — считают, что программное обеспечение для их нестандартной фильтрации лучше содержащегося в обычных интегральных микросхемах цифровых фильтров. В частности, большинство нестандартных цифровых фильтров оптимизированы по параметрам работы во временной области, а не в частотной. Например, процессоры «Wadia» превосходно ведут себя во временной области, — их отличает почти безупречное воссоздание прямоугольных импульсов и отсутствие предварительного и последующего эха в импульсном отклике. Такие прекрасные свойства во временной области порой достигаются ценой некоторого спада в полосе звуковых частот. Фильтры «Wadia» обладают спадом около 3 дБ на частоте 20 кГц. Процессор «The Meitner Intelligent Digital Audio Translator» (IDAT) использует комбинацию фильтров, чтобы добиться идеальных характеристик как во временной, так и в частотной областях

В некоторых цифровых процессорах используются так называемые однобитные ЦАП’ы, которые правильнее называть ЦАП’ами с формированием шума, делъта-сигма-ЦАП’ами или ЦАП’ами с передискретизацией. Эти преобразователи также известны по их торговым маркам: «Bitstream» (фирмы «Philips»), «MASH» («Matsushita», разработка «Nippon Telephone and Telegraph»), а также «РЕМ» (разработка ,JVC»). Все эти преобразователи работают по одному и тому же принципу: для преобразования двоичного кода в аналоговый сигнал вместо резисторной матрицы с различными весами битов однобитный ЦАП использует только два состояния — ноль и единицу. Однобитный код — это серия изменяющихся по продолжительности импульсов постоянной амплитуды. От ширины импульса зависит напряжение на аналоговом выходе. Этим объясняется, почему однобитное кодирование называют также широтно-импульсной модуляцией.

Однобитный код достаточно высокочастотный (кратность передискретизации от 64 до 256), благодаря чему возможно восстановление звукового сигнала из двух логических состояний при помощи схемы с коммутируемым конденсатором. Поэтому однобитный ЦАП не требует такой точности, как ЦАП’ы на основе резисторной матрицы. В ЦАП’ах с передискретизацией амплитудное разрешение заменяется на разрешение по времени. По природе своей они имеют хорошую линейность и без подстройки MSB (собственно, MSB там и нет). ЦАП’ы с передискретизацией не требуют и преобразователя тока в напряжение.

www.hifiaudio-spb.ru

ЦАП — это… Что такое ЦАП?

ЦАП — Центр автомобилестроительных программ авто Словарь: С. Фадеев. Словарь сокращений современного русского языка. С. Пб.: Политехника, 1997. 527 с. ЦАП центральный артиллерийский пост на корабле воен., морск. Словари: Словарь сокращений и… … Словарь сокращений и аббревиатур

ЦАП — ЦАП, в знач. сказуемого (прост.). Цапнул. «Кто то цап за плечо: держи вора! кричит.» Некрасов. «Мещанин цап его да и швырнул за перегородку.» Лесков. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 … Толковый словарь Ушакова

Цап — I предик. разг.; = царап, цап царап Обозначение быстрого хватательного движения как действия. II межд. разг.; = царап, цап царап Употребляется при обозначении, при передаче быстрого хватательного действия. Толковый словарь Ефремовой. Т. Ф.… … Современный толковый словарь русского языка Ефремовой

цап — межд. в функц. сказ. Разг. сниж. Употр. для обозначения быстрого действия (по зн. цапать цапнуть). Цап книжку и не отдаёт. Кот цап меня за пятку … Энциклопедический словарь

Цап — ЦАПЕНКО ЦЮПА В украинском языке множество нарицательных существительных и прилагательных используется в качестве фамилии без какого либо специального суффикса: Цап козел , Цюпа конура . (У) Цапенко украинская фамилия с типичным суффиксом енко. Но … Русские фамилии

ЦАП — ЦАП, в знач. сказ. (разг.). Цапнул. Ц. его за руку. Ц. яблоко из рук. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова

ЦАП — ЦАП, см. цапать. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля

цап — См … Словарь синонимов

цап — цап, неизм … Русский орфографический словарь

цап — См. Сап … Исторический словарь галлицизмов русского языка

dic.academic.ru