Модель и – Модель — Википедия

МОДЕЛЬ — это… Что такое МОДЕЛЬ?

модель — и, ж. modèle m., ит. modello, нем. Model, пол. model. 1. Образец, с которого снимается форма для отливки или воспроизведения в другом материале. БАС 1. Точить модель посуды, наводить резьбы, делать формы 15. 11. 1717. Контракт с Антонио Бонавери …   Исторический словарь галлицизмов русского языка

Модель AD-AS — (модель совокупного спроса и совокупного предложения)  макроэкономическая модель, рассматривающая макроэкономическое равновесие в условиях изменяющихся цен в краткосрочном и долгосрочном периодах …   Википедия

МОДЕЛЬ — 1) воспроизведение предмета в уменьшенных размерах; 2) натурщик, служащий образцом при живописи или скульптуре; 3) образец, по которому изготовляют какое либо изделие. Словарь иностранных слов, вошедших в состав русского языка. Павленков Ф., 1907 …   Словарь иностранных слов русского языка

Модель А — используемая в соционике модель функционирования психики человека. Эта модель гипотетически выделяет в психике восемь функций, схематически располагаемых в виде прямоугольника 2х4 в четырёх горизонтальных уровнях и двух вертикальных блоках.… …   Википедия

МОДЕЛЬ — [дэ], модели, жен. (франц. modele). 1. Образец, образцовый экземпляр какого нибудь изделия (спец.). Модель товара. Модель платья. 2. Воспроизведенный, обычно в уменьшенном виде, образец какого нибудь сооружения (тех.). Модель машины. 3. Тип,… …   Толковый словарь Ушакова

модель — См. пример …   Словарь синонимов

модель — Масштабный предметный образец объекта или его частей, отображающий их строение и действие [Терминологический словарь по строительству на 12 языках (ВНИИИС Госстроя СССР)] модель Представление системы, процесса, ИТ услуги, конфигурационной единицы …   Справочник технического переводчика

МОДЕЛЬ — (model) Упрощенная система, используемая для имитирования определенных аспектов реальной экономики. Экономическая теория вынуждена использовать упрощенные модели: реальная мировая экономика настолько велика и сложна, что ее просто невозможно… …   Экономический словарь

МОДЕЛЬ —         (франц. modele, от лат. modulus мера, образец, норма), в логике и методологии науки аналог (схема, структура, знаковая система) определ. фрагмента природной или социальной реальности, порождения человеч. культуры, концептуально теоретич.… …   Философская энциклопедия

МОДЕЛЬ — абстрактное или вещественное отображение объектов или процессов, адекватное исследуемым объектам (процессам) в отношении некоторых заданных критериев. Напр., математическая модель слоенакопления (абстрактная модель процесса), блок диаграмма… …   Геологическая энциклопедия

МОДЕЛЬ IS-LM — (IS LM model) Модель, которая часто используется в качестве исключительно простого примера общего равновесия (general equilibrium) в макроэкономике. Кривая IS показывает сочетания национального дохода Y и процентной ставки r, при которых… …   Экономический словарь

dic.academic.ru

виды моделей, понятие и описание

Каждый современный человек ежедневно сталкивается с понятиями «объект» и «модель». Примерами объектов являются как предметы, доступные для осязания (книга, земля, стол, ручка, карандаш), так и недоступные (звезды, небо, метеориты), предметы художественного творчества и умственной деятельности (сочинение, стихотворение, решение задачи, картина, музыка и другие). Причем каждый объект человеком воспринимается только как единое целое.

Объект. Виды. Характеристики

Исходя из вышесказанного, можно сделать вывод, что объект является частью внешнего мира, которая может быть воспринята в качестве единого целого. Каждый предмет восприятия имеет свои индивидуальные характеристики, отличающие его от других (форма, сфера использования, цвет, запах, размер и так далее). Важнейшей характеристикой объекта является название, но для полного качественного его описания одного названия недостаточно. Чем более полно и подробно описан объект, тем легче процесс его распознавания.

Модели. Определение. Классификация

В своей деятельности (образовательной, научной, художественной, технологической) человек ежедневно использует уже существующие и создает новые модели внешнего мира. Они позволяют сформировать впечатление о процессах и объектах, недоступных для непосредственного восприятия (очень маленькие или, наоборот, очень большие, очень медленные или очень быстрые, очень далекие и так далее).

Итак, модель – это некоторый объект, отражающий важнейшие особенности изучаемого явления, объекта либо процесса. Может существовать несколько вариаций моделей одного и того же объекта, также как несколько объектов могут быть описаны одной единственной моделью. Например, подобная ситуация возникает в механике, когда различные тела с материальной оболочкой могут быть выражены материальными точками, то есть одинаковой моделью (человек, автомобиль, поезд, самолет).

Важно помнить, что ни одна модель не способна полноценно заменить изображаемый объект, так как она отображает только некоторые из его свойств. Но порой при решении определенных задач различных научных и промышленных течений описание внешнего вида модели может быть не просто полезным, но единственной возможностью представить и изучить особенности характеристик объекта.

Сфера применения предметов моделирования

Модели играют важную роль в различных сферах жизни человека: в науке, образовании, торговле, проектировании и других. Например, без их применения невозможны проектирование и сборка технических устройств, механизмов, электрических цепей, машин, зданий и так далее, так как без предварительных расчетов и создания чертежа выпуск даже простейшей детали невозможен.

Часто используются модели в образовательных целях. Они носят названия наглядных. Например, из географии представление о Земле как о планете человек получает, изучая глобус. Также актуальными наглядные модели являются и в других науках (химии, физике, математике, биологии и других).

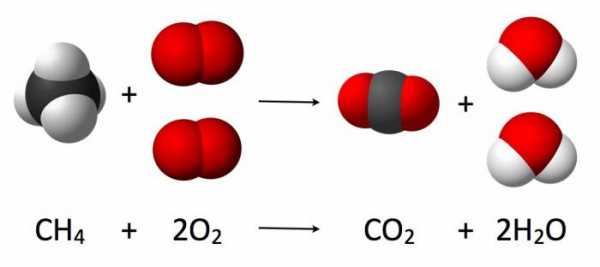
В свою очередь, теоретические модели востребованы при изучении естественных и точных наук (биологии, химии, физики, геометрии). Они отражают свойства, поведение и строение объектов, подвергающихся изучению.

Моделирование как процесс

Моделирование – метод познавания, включающий в себя исследование существующих и создание новых моделей. Предметом познания данной науки является модель. Виды моделей ранжируются в зависимости от различных свойств. Как известно, любой объект имеет множество характеристик. При создании определенной модели выделяются лишь наиболее важные для решения поставленной задачи.

Процессом создания моделей является художественное творчество во всем своем разнообразии. В связи с этим фактически каждое художественное или литературное произведение можно рассматривать в качестве модели реального объекта. Например, картины являются моделями реальных пейзажей, натюрмортов, людей, литературные произведения – моделями человеческих жизней и так далее. Например, при создании модели самолета с целью изучения его аэродинамических качеств важно отразить в ней геометрические свойства оригинала, но абсолютно неважен его цвет.

Одни и те же объекты различными науками изучаются с разных точек зрения, а соответственно, их виды моделей для изучения будут также отличаться. Например, физика изучает процессы и результаты взаимодействия объектов, химия – химический состав, биология – поведение и строение организмов.

Модель относительно временного фактора

Относительно времени модели делятся на два вида: статические и динамические. Примером первого вида является единоразовое обследование человека в клинике. Оно отображает картину его состояния здоровья на данный момент, в то время как его медицинская карта будет моделью динамической, отражающей изменения, происходящие в организме на протяжении определенного периода времени.

Модель. Виды моделей относительно формы

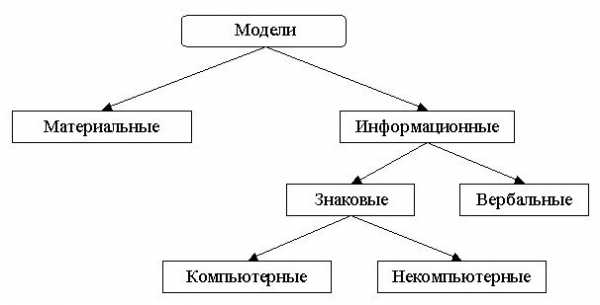
Как уже понятно, модели могут различаться по разным характеристикам. Так, все ныне известные виды моделей данных можно условно разделить на два основных класса: материальные (предметные) и информационные.

Первый вид передает физические, геометрические и иные свойства объектов в материальной форме (анатомический муляж, глобус, макет здания и так далее).

Виды информационных моделей разнятся по форме реализации: знаковая и образная. Образные модели (фотографии, рисунки и другое) являются зрительными реализациями объектов, зафиксированными на определенном носителе (фото-, кинопленке, бумажном или цифровом).

Они широко применяются в образовательном процессе (плакаты), при изучении различных наук (ботаника, биология, палеонтология и других). Знаковые модели – это реализации объектов в виде символов одной из известных языковых систем. Они могут быть представлены в виде формул, текста, таблиц, схем и так далее. Существуют случаи, когда, создавая знаковую модель (виды моделей передают конкретно то содержание, которое требуется для изучения определенных характеристик объекта), используют сразу несколько известных языков. Примером в данном случае выступают различные графики, диаграммы, карты и подобное, где используются как графические символы, так и символы одной из языковых систем.

С целью отражения сведений из различных сфер жизни применяются три основных вида информационных моделей: сетевые, иерархические и табличные. Из них наиболее популярным является последний, применяемый для фиксации различных состояний объектов и характерных для них данных.

Табличная реализация модели

Данный вид информационной модели, как уже было сказано выше, является наиболее известным. Выглядит он следующим образом: это обычная, состоящая из строк и столбцов таблица прямоугольной формы, графы которой заполнены символами одного из известных знаковых языков мира. Применяются табличные модели с целью характеристики объектов, обладающих одинаковыми свойствами.

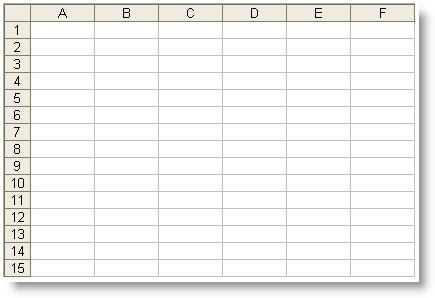С их помощью в различных научных сферах могут быть созданы как динамические, так и статические модели. Например, таблицы, содержащие математические функции, различные статистические данные, расписания поездов и так далее.

Математическая модель. Виды моделей

Отдельной разновидностью информационных моделей являются математические. Все виды математических моделей обычно состоят из уравнений, написанных на языке алгебры. Решение данных задач, как правило, основывается на процессе поиска равнозначных преобразований, которые способствуют выражению переменной величины в виде формулы. Существуют также для некоторых уравнений и точные решения (квадратные, линейные, тригонометрические и так далее). Как следствие, для их решения приходится применять методы решения с приближенной заданной точностью, иначе говоря, такие виды математических данных, как числовой (метод половинного деления), графический (построение графиков) и другие. Метод половинного деления целесообразно использовать лишь при условии, что известен отрезок, где функция при определенных значениях корня уравнения принимает полярные значения.

А метод построения графика является унифицированным. Его можно использовать как в вышеописанном случае, так и в ситуации, когда решение может быть только приближенным, а не точным, в случае так называемого «грубого» решения уравнений.

fb.ru

Моделирование — Википедия

Модели́рование — исследование объектов познания на их моделях; построение и изучение моделей реально существующих объектов, процессов или явлений с целью получения объяснений этих явлений, а также для предсказания явлений, интересующих исследователя.

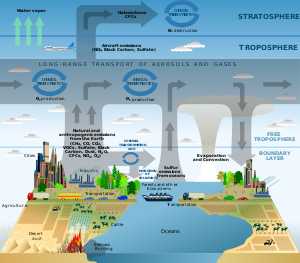Пример результата научного моделирования. Схема химических процессов и процессов переноса в атмосфере.

В силу многозначности понятия «модель» в науке и технике не существует единой классификации видов моделирования: классификацию можно проводить по характеру моделей, по характеру моделируемых объектов, по сферам приложения моделирования (в технике, физических науках, кибернетике и т. д.).

В настоящее время по технологии моделирования и области применения выделяют такие основные виды моделирования:

и др.

Процесс моделирования включает три элемента:

• субъект (исследователь),
• объект исследования,
• модель, определяющую (отражающую) отношения познающего субъекта и познаваемого объекта.

Первый этап построения модели предполагает наличие некоторых знаний об объекте-оригинале. Познавательные возможности модели обуславливаются тем, что модель отображает (воспроизводит, имитирует) какие-либо существенные черты объекта-оригинала. Вопрос о необходимой и достаточной мере сходства оригинала и модели требует конкретного анализа. Очевидно, модель утрачивает свой смысл как в случае тождества с оригиналом (тогда она перестаёт быть моделью), так и в случае чрезмерного во всех существенных отношениях отличия от оригинала. Таким образом, изучение одних сторон моделируемого объекта осуществляется ценой отказа от исследования других сторон. Поэтому любая модель замещает оригинал лишь в строго ограниченном смысле. Из этого следует, что для одного объекта может быть построено несколько «специализированных» моделей, концентрирующих внимание на определённых сторонах исследуемого объекта или же характеризующих объект с разной степенью детализации.

На втором этапе модель выступает как самостоятельный объект исследования. Одной из форм такого исследования является проведение «модельных» экспериментов, при которых сознательно изменяются условия функционирования модели и систематизируются данные о её «поведении». Конечным результатом этого этапа является множество (совокупность) знаний о модели.

На третьем этапе осуществляется перенос знаний с модели на оригинал — формирование множества знаний. Одновременно происходит переход с «языка» модели на «язык» оригинала. Процесс переноса знаний проводится по определённым правилам. Знания о модели должны быть скорректированы с учётом тех свойств объекта-оригинала, которые не нашли отражения или были изменены при построении модели.

Четвёртый этап — практическая проверка получаемых с помощью моделей знаний и их использование для построения обобщающей теории объекта, его преобразования или управления им.

Моделирование — циклический процесс. Это означает, что за первым четырёхэтапным циклом может последовать второй, третий и т. д. При этом знания об исследуемом объекте расширяются и уточняются, а исходная модель постепенно совершенствуется. Недостатки, обнаруженные после первого цикла моделирования, обусловленные малым знанием объекта или ошибками в построении модели, можно исправить в последующих циклах.

Сейчас трудно указать область человеческой деятельности, где не применялось бы моделирование. Разработаны, например, модели производства автомобилей, выращивания пшеницы, функционирования отдельных органов человека, жизнедеятельности Азовского моря, последствий атомной войны. В перспективе для каждой системы могут быть созданы свои модели, перед реализацией каждого технического или организационного проекта должно проводиться моделирование.

Моделирование для прямых измерений и экспериментов[править | править код]

Модели обычно используются, когда невозможно или непрактично создавать экспериментальные условия, при которых учёные могут непосредственно измерять результаты. Прямое измерение результатов в контролируемых условиях (см. Научный метод) всегда будет более надёжным, чем смоделированные оценки результатов.

В моделировании и симуляции модель представляет собой целенаправленное упрощение и абстрагирование восприятия реальности, обусловленное физическими и когнитивными ограничениями.^[1] Моделирование — управляемая задача, потому что модель направлена на решения определённых заданных вопросов или задач.

Упрощения призваны опустить все известные и наблюдаемые сущности и их отношения, которые не важны для рассматриваемой задачи. Абстракция агрегирует информацию, которая важна, но не нужна в той же детализации, что и объект исследования. Оба действия, упрощение и абстракция выполняются целенаправленно. Однако они сделаны на основе восприятия реальности. Это восприятие уже само по себе является моделью, поскольку оно связано с физическими ограничениями.

Существуют также ограничения на то, что мы можем формально наблюдать с помощью нашего текущего инструментария и методов, а также в виде когнитивных барьеров, которые ограничивают то, что мы можем объяснить существующими научными теориями. Такая модель включает сущности, их поведение и их формальные отношения и часто упоминается как концептуальная модель. Чтобы создать такую модель, она должна быть реализована через компьютерное моделирование. Для этого требуется большая выборка через применение, например численной аппроксимации или использование эвристики.^[2] Несмотря на все эти эпистемологические и вычислительные ограничения, симуляция была признана в качестве одного из трёх ключевых компонентов научных методов: построение теории, моделирование и экспериментирование.

[3]

Симуляция[править | править код]

Симуляция — это комплексные процессы поведения модели в рамках заданных условий моделирования. Статичная симуляция предоставляет информацию о системе в определённый заданный момент времени (обычно при равновесии, если такое состояние существует). Динамическая симуляция предоставляет информацию в ходе течения времени. Симуляция приводит модель к жизни и показывает, как будет вести себя конкретный объект или явление. Симуляция может быть полезна для тестирования, анализа или обучения в тех случаях, когда модели или концепции реального мира

могут быть представлены в виде их моделей.[4]

Структура[править | править код]

Структура является фундаментальным, но зачастую неосязаемым понятием, которое вбирает в себя распознавание, наблюдение, генезис, сохранение постоянства закономерностей и отношений моделируемых сущностей. От словесного описания ребёнком снежинки до детального научного анализа свойств магнитных полей, понятие структуры является основой почти каждого способа исследования и открытия в науке, философии и искусстве.^[5]

Системы[править | править код]

Система представляет собой набор взаимодействующих или взаимозависимых сущностей, реальных или абстрактных, образующих интегрированное целое. В общем, система представляет собой конструкцию или набор различных элементов, которые вместе могут приводить к результатам, которые не могут быть получены только самими элементами.^[6] Концепцию «интегрированного целого» можно также сформулировать в терминах системы, воплощающей набор отношений, которые отличаются от отношений множества к другим элементам и от отношений между элементом множества и элементами, не входящими в состав реляционного режима. Существует два типа системных моделей: 1) дискретный, в котором переменные мгновенно меняются в отдельные моменты времени и 2) непрерывный, когда переменные состояния непрерывно изменяются по времени.^[7]

Создание модели[править | править код]

Моделирование — это процесс создания модели как концептуального представления некоторого явления. Обычно модель будет иметь дело только с некоторыми аспектами рассматриваемого явления, и две модели одного и того же явления могут существенно отличаться, т.е. различия между ними будут не только в простом переименовании их составляющих компонентов.

Такие отличия могут быть вызваны различными требованиями конечных пользователей данной модели или концептуальными или эстетическими отличительными предпочтениями создателей модели и их решениями, принятыми в ходе процесса моделирования. Соображения создателей, которые могут повлиять на структуру модели, могут быть в области личных профессиональных предпочтений для, например, применения сокращённой онтологии, или предпочтений в отношении применения статистических моделей по сравнению с детерминированными, дискретных по сравнению с непрерывными и т. д. В любом случае пользователям модели необходимо понять сделанные создателями предположения, которые направлены на то или иное использование модели.

Для построения модели требуется абстракция. Предположения используются в моделировании, чтобы указать область применения модели. Например, специальная теория относительности принимает инерциальную систему отсчёта. Это предположение было контекстуализировано и далее объяснено общей теорией относительности. Модель делает точные предсказания, когда её допущения действительны и, с большой вероятностью, не дают точных прогнозов, когда её предположения не выполняются. Такие предположения часто совпадают с тем моментом, когда старые теории сменяются новыми (к слову, общая теория относительности работает и в неинерциальных системах отсчёта).

Оценка модели[править | править код]

Модель оценивается в первую очередь по её согласованности с эмпирическими данными; любая модель, несовместимая с воспроизводимыми наблюдениями, должна быть изменена или отклонена. Один из способов изменить модель — это ограничение области применения, над которой она совпадает с наблюдениями с высокой степенью достоверности. Например, ньютоновская физика, которая очень полезна, за исключением очень малых, очень быстрых и очень массивных явлений мира. Тем не менее, соответствие только эмпирическим данным недостаточно для того, чтобы модель была принята как действительная. Другие факторы, важные при оценке модели, включают:

• Возможность объяснения прошлых наблюдений

• Возможность прогнозирования будущих наблюдений

• Стоимость использования, особенно в сочетании с другими моделями

• Опровержимость, позволяющая оценить степень достоверности модели

• Простота или даже эстетическая привлекательность

Исходя из перечисленных критериев, пользователь модели может попытаться количественно оценить её с помощью функции полезности, определив для себя приоритетность (веса) переменных.

Визуализация[править | править код]

Визуализация — это любой способ создания изображений, диаграмм или анимаций для коммуникационного сообщения. Визуализация с помощью образов была эффективным способом коммуникационного обмена как абстрактными, так и конкретными идейными сущностями с самого начала истории человечества — пещерные картины, египетские иероглифы, греческая геометрия и революционные методы технического перевода Леонардо да Винчи для инженерных и научных задач.

Пространственный маппинг[править | править код]

Пространственный маппинг относится к методологии, в которой используется «квази-глобальная» методика для увязки сопутствующей «грубой» (идеальной или с низкой точностью) с «высокоточной» (практической или с высокой точностью) моделями различных сложностей. В инженерной оптимизации маппинг выравнивает (отображает) очень быстро грубую модель с её связанной дорогостоящей вычислительной высокоточной моделью, чтобы избежать прямой дорогостоящей процедуры оптимизации такой модели. Процесс маппинга итеративно уточняет грубую модель (суррогатная модель) сопоставляя её с высокоточной.

1. ↑ Tolk, A. Learning something right from models that are wrong – Epistemology of Simulation (En) // Concepts and Methodologies in Modeling and Simulation. Springer–Verlag. — 2015. — С. pp. 87–106.
2. ↑ Oberkampf, W. L., DeLand, S. M., Rutherford, B. M., Diegert, K. V., & Alvin, K. F. Error and uncertainty in modeling and simulation (En) // Reliability Engineering & System Safety 75(3). — 2002. — № 75(3). — С. 333–57.
3. ↑ Ihrig, M. A New Research Architecture For The Simulation Era (En) // European Council on Modelling and Simulation. — 2012. — С. pp. 715–20.
4. ↑ DEFENSE ACQUISITION UNIVERSITY PRESS FORT BELVOIR, VIRGINIA. SYSTEMS ENGINEERING FUNDAMENTALS. — 2001.
5. ↑ Pullan Wendy. Structure. — Cambridge: Cambridge University Press. — 2000. — ISBN 0-521-78258-9.
6. ↑ Fishwick PA. Simulation Model Design and Execution: Building Digital Worlds. — Upper Saddle River, NJ: Prentice Hall.. — 1995.
7. ↑ Sokolowski, J.A., Banks, C.M. Principles of Modelling and Simulation. — Hoboken, NJ: John Wiley and Sons.. — 2009.

• Глинский Б. А. Моделирование как метод научного исследования. М., 1965;
• Кодрянц И. Г. Философские вопросы математического моделирования. Кишинев, 1978;
• Мамедов Н. М. Моделирование и синтез знаний. Баку, 1978;
• Самарский А. А., Михайлов А. П. Математическое моделирование: Идеи. Методы. Примеры. — М.: Наука, 1997. — 320 с. — ISBN 5-9221-0120-X.
• Уемов А. И. Логические основы метода моделирования. М., 1971
• Аристов А. О. Теория квазиклеточных сетей : научная монография — М: МИСиС, 2014. — 188с. ISBN 978-5-600-00321-7
• Кононюк А. Е. Обобщённая теория моделирования. Начала. К.1. Ч.1. «Освіта України», 2012. — 602 с. ISBN 978-966-7599-50-8

ru.wikipedia.org

Модели и моделирование

1. 1. Понятие модели и моделирования. Классификация видов моделирования и моделей систем

При использовании метода моделирования свойства и поведение объекта изучают путем применения вспомогательной системы – модели, находящейся в определенном объективном соответствии с исследуемым объектом.

Под объектом исследования понимается либо некоторая система, элементы которой в процессе достижения конечной цели реализуют один или несколько процессов, либо некоторый процесс, реализуемый элементами одной или нескольких систем. В связи с этим в дельнейшем тексте термины «модель объекта», «модель системы», «модель процесса» следует воспринимать как эквивалентные.

Представления о тех или иных свойствах объектов, их взаимосвязях формируются исследователем в виде описания этих объектов на обычном языке, в виде рисунков, графиков, формул или реализуются в виде макетов и других устройств. Подобные способы описания обобщаются в едином понятии – модель, а построение и изучение моделей называетсямоделированием.

Заслуживает предпочтения следующее определение: модель – объект любой природы, который создается исследователем с целью получения новых знаний об объекте-оригинале и отражает только существенные (с точки зрения разработчика) свойства оригинала.

Модель считается адекватнойобъекту-оригиналу, если она с достаточной степенью приближения на уровне понимания моделируемого процесса исследователем отражает закономерности процесса функционирования реальной системы во внешней среде.

Модели позволяют вынести упрощенное представление о системе и получить некоторые результаты намного проще, чем при изучении реального объекта. Более того, гипотетически модели объекта могут быть исследованы и изучены перед тем, как объект будет создан.

В практике исследования производственно-экономических объектов модели могут применяться для самых разных целей, что вызывает использование моделей различных классов. Построение одной-единственной математической модели для сложной производственной системы практически не представляется возможным без разработки вспомогательных моделей. Поэтому, как правило, при создании конечной математической модели исследуемого объекта строят частные вспомогательные модели, отражающие ту или иную информацию об объекте, имеющуюся у разработчика на данном этапе построения модели.

В основе моделирования лежит теория подобия, которая утверждает, что абсолютное подобие может иметь место лишь при замене одного объекта другим точно таким же. При моделировании абсолютное подобие не имеет места и стремятся к тому, чтобы модель достаточно хорошо отображала исследуемую сторону функционирования объекта.

Классификационные признаки. В качестве одного из первых признаков классификации видов моделирования можно выбрать степень полноты модели и разделить модели в соответствии с этим признаком на полные, неполные и приближенные. В основе полного моделирования лежит полное подобие, которое проявляется как во времени, так и в пространстве. Для неполного моделирования характерно неполное подобие модели изучаемому объекту. В основе приближенного моделирования лежит приближенное подобие, при котором некоторые стороны функционирования реального объекта не моделируются совсем. Классификация видов моделирования системS приведена на рис.1.1.

В зависимости от характера изучаемых процессов в системе Sвсе виды моделирования могут быть разделены на детерминированные и стохастические, статические и динамические, дискретные, непрерывные и дискретно-непрерывные.Детерминированное моделированиеотображает детерминированные процессы, т.е. процессы, в которых предполагается отсутствие всяких случайных воздействий;стохастическое моделированиеотображает вероятностные процессы и события. В этом случае анализируется ряд реализаций случайного процесса и оцениваются средние характеристики, т.е. набор однородных реализаций.Статическое моделированиеслужит для описания поведения объекта в какой-либо момент времени, адинамическое моделированиеотражает поведение объекта во времени.Дискретное моделированиеслужит для описания процессов, которые предполагаются дискретными, соответственно непрерывное моделирование позволяет отразить непрерывные процессы в системах, адискретно-непрерывное моделированиеиспользуется для тех случаев, когда хотят выделить наличие как дискретных, так и непрерывных процессов.

В зависимости от формы представления объекта (системы S) можно выделить мысленное и реальное моделирование.

Мысленное моделирование часто является единственным способом моделирования объектов, которые либо практически нереализуемы в заданном интервале времени, либо существуют вне условий, возможных для их физического создания. Например, на базе мысленного моделирования могут быть проанализированы многие ситуации микромира, которые не поддаются физическому эксперименту. Мысленное моделирование может быть реализовано в виде наглядного, символического и математического.

Рис. 1.1. Классификация видов моделирования систем

При наглядном моделированиина базе представлений человека о реальных объектах создаются различные наглядные модели, отображающие явления и процессы, протекающие в объекте. В основугипотетического моделированияисследователем закладывается некоторая гипотеза о закономерностях протекания процесса в реальном объекте, которая отражает уровень знаний исследователя об объекте и базируется на причинно-следственных связях между входом и выходом изучаемого объекта. Гипотетическое моделирование используется, когда знаний об объекте недостаточно для построения формальных моделей.

Аналоговое моделированиеосновывается на применении аналогий различных уровней. Наивысшим уровнем является полная аналогия, имеющая место только для достаточно простых объектов. С усложнением объекта используют аналогии последующих уровней, когда аналоговая модель отображает несколько либо только одну сторону функционирования объекта.

Существенное место при мысленном наглядном моделировании занимает макетирование. Мысленный макет может применяться в случаях, когда протекающие в реальном объекте процессы не поддаются физическому моделированию, либо может предшествовать проведению других видов моделирования. В основе построения мысленных макетов также лежат аналогии, однако обычно базирующиеся на причинно-следственных связях между явлениями и процессами в объекте. Если ввести условное обозначение отдельных понятий, т.е. знаки, а также определенные операции между этими знаками, то можно реализоватьзнаковое моделированиеи с помощью знаков отображать набор понятий – составлять отдельные цепочки из слов и предложений. Используя операции объединения, пересечения и дополнения теории множеств, можно в отдельных символах дать описание какого-то реального объекта.

В основе языкового моделированиялежит некоторый тезаурус. Последний образует из наборов входящих понятий, причем этот набор должен быть фиксированным. Следует отметить, что между тезаурусом и обычным словарем имеются принципиальные различия. Тезаурус – словарь, который очищен от неоднозначности, т.е. в нем каждому слову может соответствовать лишь единственное понятие, хотя в обычном словаре одному слову могут соответствовать несколько понятий.

Символическое моделирование представляет собой искусственный процесс создания логического объекта, который замещает реальный и выражает основные свойства его отношений с помощью определенной системы знаков и символов.

Математическое моделирование. Для исследования характеристик процесса функционирования любой системыSматематическими методами, включая и машинные, должна быть проведена формализация этого процесса, т.е. построена математическая модель.

Под математическим моделированием будем понимать процесс установления соответствия данному реальному объекту некоторого математического объекта, называемого математической моделью, и исследование этой модели, позволяющее получать характеристики рассматриваемого реального объекта. Вид математической модели зависит как от природы реального объекта, так и задач исследования объекта и требуемой достоверности и точности решения этой задачи. Любая математическая модель, как и всякая другая, описывает реальный объект лишь с некоторой степенью приближения к действительности. Математическое моделирование для исследования характеристик процесса функционирования систем можно разделить на аналитическое, имитационное и комбинированное.

Для аналитическогомоделирования характерно то, что процессы функционирования элементов системы записываются в виде некоторых функциональных соотношений (алгебраических, интегродифференциальных, конечно-разностных и т.п.) или логических условий.Аналитическая модельможет быть исследована следующими методами: а) аналитическим, когда стремятся получить в общем виде явные зависимости для искомых характеристик; б) численным, когда, не умея решать уравнения в общем виде, стремятся получить числовые результаты при конкретных начальных данных; в) качественным, когда, не имея решения в явном виде, можно найти некоторые свойства решения (например, оценить устойчивость решения).

Наиболее полное исследование процесса функционирования системы можно провести, если известны явные зависимости, связывающие искомые характеристики с начальными условиями, параметрами и переменными системы S. Однако такие зависимости удается получить только для сравнительно простых систем. При усложнении систем исследование их аналитическим методом наталкивается на значительные трудности, которые часто бывают непреодолимыми. Поэтому, желая использовать аналитический метод, в этом случае идут на существенное упрощение первоначальной модели, чтобы иметь возможность изучить хотя бы общие свойства системы. Такое исследование на упрощенной модели аналитическим методом помогает получить ориентировочные результаты для определения более точных оценок другими методами. Численный метод позволяет исследовать по сравнению с аналитическим методом более широкий класс систем, но при этом полученные решения носят частный характер. Численный метод особенно эффективен при использовании ЭВМ.

В отдельных случаях исследования системы могут удовлетворить и те выводы, которые можно сделать при использовании качественного метода анализа математической модели. Такие качественные методы широко используются, например, в теории автоматического управления для оценки эффективности различных вариантов систем управления.

В настоящее время распространены методы машинной реализации исследования характеристик процесса функционирования больших систем. Для реализации математической модели на ЭВМ необходимо построить соответствующий моделирующий алгоритм.

При имитационном моделированииреализующий модель алгоритм воспроизводит процесс функционирования системыSво времени, причем имитируются элементарные явления, составляющие процесс с сохранением их логической структуры и последовательности протекания во времени, что позволяет по исходным данным получить сведения о состояниях процесса в определенные моменты времени, дающие возможность оценить характеристики системыS.

Основным преимуществом имитационного моделирования по сравнению с аналитическим является возможность решения более сложных задач. Имитационные модели позволяют достаточно просто учитывать такие факторы, как наличие дискретных и непрерывных элементов, нелинейные характеристики элементов системы, многочисленные случайные воздействия и др., которые часто создают трудности при аналитических исследованиях. В настоящее время имитационное моделирование – наиболее эффективный метод исследования больших систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапах ее проектирования.

Когда результаты, полученные при воспроизведении на имитационной модели процесса функционирования системы S,Являются реализациями случайных величин и функций, тогда для нахождения характеристик процесса требуется его многократное воспроизведение с последующей статистической обработкой информации и целесообразно в качестве метода машинной реализации имитационной модели использовать метод статистического моделирования. Первоначально был разработан метод статистических испытаний, представляющий собой численный метод, который применялся для моделирования случайных величин и функций, вероятностные характеристики которых совпадали с решениями аналитических задач (такая процедура получила название метода Монте-Карло). Затем этот прием стали применять и для машинной имитации с целью исследования характеристик процессов функционирования систем, подверженных случайным воздействиям, т.е. появился метод статистического моделирования. Таким образом,методом статистического моделированиябудем в дальнейшем называть метод машинной реализации имитационной модели, аметодом статистических испытаний (Монте-Карло)– численный метод решения аналитической задачи.

Метод имитационного моделирования позволяет решать задачи анализа больших систем S, включая задачи оценки: вариантов структуры системы, эффективности различных алгоритмов управления системой, влияния изменения различных параметров системы. Имитационное моделирование может быть положено также в основу структурного, алгоритмического и параметрического синтеза больших систем, когда требуется создать систему, с заданными характеристиками при определенных ограничениях, которая является оптимальной по некоторым критериям оценки эффективности.

При решении задач машинного синтеза систем на основе их имитационных моделей помимо разработки моделирующих алгоритмов для анализа фиксированной системы необходимо также разработать алгоритмы поиска варианта системы. Бале в методологии машинного моделирования будем различать два основных раздела: статику и динамику, – основным содержанием которых являются соответственно вопросы анализа и синтеза систем, заданных моделирующими алгоритмами.

Комбинированное (аналитико-имитационное) моделированиепри анализе и синтезе систем позволяет объединить достоинства аналитического и имитационного моделирования. При построении комбинированных моделей проводится предварительная декомпозиция процесса функционирования объекта на составляющие подпроцессы и для тех из них, где это возможно, используются аналитические модели. Такой комбинированный подход позволяет охватить качественно новые классы систем, которые не могут быть исследованы с использованием только аналитического и имитационного моделирования в отдельности.

Другие виды моделирования. Приреальном моделированиииспользуется возможность исследования различных характеристик либо на реальном объекте целиком, либо на его части. Такие исследования могут проводиться как на объектах, работающих в нормальных режимах, так и при организации специальных режимов для оценки интересующих исследователя характеристик (при других значениях переменных и параметров, в другом масштабе времени и т.п.). Реальное моделирование является наиболее адекватным, но при этом его возможности с учетом особенностей реальных объектов ограничены. Например, проведение реального моделирования АСУ предприятием потребует, во-первых, создания такой АСУ, а во-вторых, проведения экспериментов с управляемым объектом, т.е. предприятием, что в большинстве случаев невозможно.

К основным разновидностям реального моделирования относятся:

• Натурное моделирование, под которым понимают проведение исследования на реальном объекте с последующей обработкой результатов эксперимента на основе теории подобия. При функционировании объекта в соответствии с поставленной целью удается выявить закономерности протекания реального процесса. Необходимо отметить, что такие разновидности натурного эксперимента, как производственный эксперимент и комплексные испытания, обладают высокой степенью достоверности.

• Физическое моделированиеотличается от натурного тем, что исследование проводится на установках, которые сохраняют природу явлений и обладают физическим подобием.

С точки зрения математического описания объекта и в зависимости от его характера модели можно разделить на модели аналоговые (непрерывные), цифровые (дискретные) и аналого-цифровые (комбинированные). Под аналоговой модельюпонимается модель, которая описывается уравнениями, связывающими непрерывные величины. Подцифровойпонимается модель, которая описывается уравнениями, связывающими дискретные величины, представленные в цифровом виде. Поданалого-цифровойпонимается модель, которая может быть описана уравнениями, связывающими непрерывные и дискретные величины.

Особое место в моделировании занимает кибернетическое моделирование, в котором отсутствует непосредственное подобие физических процессов, происходящих в моделях, реальным процессам. В этом случае стремятся отобразить лишь некоторую функцию и рассматривают реальный объект как «черный ящик», имеющий ряд входов и выходов, и моделируют некоторые связи между выходами и входами. Чаще всего при использовании кибернетических моделей проводят анализ поведенческой стороны объекта при различных воздействиях внешней среды. Таким образом, в основе кибернетических моделей лежит отражение некоторых информационных процессов управления, что позволяет оценить поведение реального объекта. Для построения имитационной модели в этом случае необходимо выделить исследуемую функцию реального объекта, попытаться формализовать эту функцию в виде некоторых операторов связи между входом и выходом и воспроизвести на имитационной модели данную функцию, причем на базе совершенно иных математических соотношений и, естественно, иной физической реализации процесса.

Целевое назначение модели.По целевому назначению модели подразделяются на модели структуры, функционирования и стоимостные (модели расхода ресурсов).

Модели структурыотображают связи между компонентами объекта и внешней средой и подразделяются на:

• каноническую модель, характеризующую взаимодействие объекта с окружением через входы и выходы;

• модель внутренней структуры, характеризующую состав компонентов объекта и связи между ними;

• модель иерархической структуры (дерево системы), в которой объект (целое) расчленяется на элементы более низкого уровня, действия которых подчинены интересам целого.

Модель структуры обычно представляется в виде блок-схемы, реже графов и матриц связей.

Модели функционированиявключают широкий спектр символических моделей, например:

модель жизненного цикла системы,описывающая процессы существования системы от зарождения замысла ее создания до прекращения функционирования;

модели операций, выполняемых объектом и представляющих описание взаимосвязанной совокупности процессов функционирования отдельных элементов объекта при реализации тех или иных функций объекта. Так, в состав моделей операций могут входить модели надежности, характеризующие выход элементов системы из строя под влиянием эксплуатационных факторов, и модели живучести факторов, характеризующие выход элементов системы из строя под влиянием целенаправленного воздействия внешней среды;

информационные модели, отображающие во взаимосвязи источники и потребители информации, виды информации, характер ее преобразования, а также временные и количественные характеристики данных;

процедурные модели,описывающие порядок взаимодействия элементов исследуемого объекта при выполнении различных операций, например обработки материалов, деятельности персонала, использования информации, в том числе и реализации процедур принятия управленческих решений;

временные модели,описывающие процедуру функционирования объекта во времени и распределение ресурса «время» по отдельным компонентам объекта.

Стоимостные модели,как правило, сопровождают модели функционирования объекта и по отношению к ним вторичны, «питаются» от них информацией и совместно с ними позволяют проводить комплексную технико-экономическую оценку объекта или его оптимизацию по экономическим критериям.

При анализе и оптимизации производственно-экономических объектов проводится объединение построенных математических функциональных моделей с математическими стоимостными моделями в единую экономико-математическую модель.

Насколько можно судить по литературным источникам общепринятой классификации моделей экономических систем пока не существует. Однако представляется достаточно полезной классификация математических моделей экономических систем, приведенная в книге Т. Нейлора «Машинные имитационные эксперименты с моделями экономических систем» (1971 г.) (рис. 1.2).

Рис.1.2. Классификация экономических моделей

Экономико-математической моделью (ЭММ)называется выражение, состоящее из совокупности связанных между собой математическими зависимостями (формулами, уравнениями, неравенствами, логическими условиями величин – факторов, все или часть которых имеют экономический смысл. По своей роли в ЭММ эти факторы целесообразно подразделить на параметры и характеристики (рис. 1.3).

Рис. 1.3. Классификация факторов по их роли в ЭВМ

При этом параметрамиобъекта называются факторы, характеризующие свойства объекта или составляющих его элементов. В процессе исследования объекта ряд параметров может изменяться, поэтому они называютсяпеременными,которые в свою очередь подразделяются на переменные состояния и переменные управления. Как правило, переменные состояния объекта являются функцией переменных управления и воздействий внешней среды.Характеристиками(выходными характеристиками) называются интересующие исследователя непосредст-венные конечные результаты функционирования объекта (естественно, что выходные характеристики являются переменными состояния). Соответственно характеристики внешней среды описывают свойства внешней среды, которые сказываются на процессе и результате функционирования объекта. Значения ряда факторов, определяющие начальное состояние объекта или внешней среды, называютсяначальными условиями.

При рассмотрении ЭММ оперируют следующими понятиями: критерий оптимальности, целевая функция, система ограничений, уравнения связи, решение модели.

Критерием оптимальностиназывается некоторый показатель, имеющий экономическое содержание, служащий формализацией конкретной цели управления и выражаемый при помощи целевой функции через факторы модели. Критерий оптимальности определяет смысловое содержание целевой функции. В ряде случаев в качестве критерия оптимальности может выступать одна из выходных характеристик объекта.

Целевая функцияматематически связывает между собой факторы модели, ее значение определяется значениями этих величин. Содержательный смысл целевой функции придает только критерий оптимальности.

Не следует смешивать критерий оптимальности и целевую функцию. Так, например, критерий прибыли и стоимости произведенной продукции могут описываться одной и той же целевой функцией:

, (1.1)

где – номенклатура производимой продукции;– объем выпускаi-ой номенклатуры;– прибыль от выпуска единицыi-ой номенклатуры или стоимость единицыi-ой номенклатуры в зависимости от смысла критерия оптимальности.

Критерий прибыли может рассчитываться и по нелинейной целевой функции:

, (1.2)

Если прибыль от выпуска единицы i-ой номенклатуры является функцией от объема выпуска.

При наличии нескольких критериев оптимальности каждый из них будет формализован своей частной целевой функцией , где– число критериев оптимальности. Для однозначного выбора оптимального решения исследователь может сформулировать новую целевую функцию

. (1.3)

Однако целевая функция может уже не нести экономического смысла, в этом случае критерий оптимальности для нее отсутствует.

Система ограниченийопределяет пределы, сужающие область осуществимых, приемлемых или допустимых решений и фиксирующие основные внешние и внутренние свойства объекта. Ограничения определяют область протекания процесса, пределы изменения параметров и характеристик объекта.

Уравнения связиявляются математической формализацией системы ограничений. Между понятиями «система ограничений» и «Уравнения связи» существует точно такая же аналогия, как между понятиями «критерий оптимальности» и «целевая функция»: различные по смыслу ограничения могут описываться одинаковыми уравнениями связи, а одно и то же ограничение в разных моделях записываться различными уравнениями связи.

Таким образом, именно критерий оптимальности и система ограничений в первую очередь определяют концепцию построения будущей математической модели, т.е. концептуальную модель, а их формализация, т.е. целевая функция и уравнения связи, представляют собой математическую модель.

Решениемматематической модели называется такой набор (совокупность) значений переменных, который удовлетворяет ее уравнениям связи. Решения, имеющие экономический смысл, называют структурно допустимыми. Модели, имеющие много решений, называются вариантными в отличие от безвариантных, имеющих одно решение. Среди структурно допустимых решений вариантной модели, как правило, находится одно решение, при котором целевая функция в зависимости от смысла модели имеет наибольшее или наименьшее значение. Такое решение, как и соответствующее значение целевой функции, называетсяоптимальным(в частности, наименьшим или наибольшим).

Использование ЭММ, особенно оптимальных, предполагает не только построение модели, соответствующей поставленной задаче, но и ее решение при помощи подходящего метода. В связи с этим иногда под моделированием (в узком смысле) понимается этап нахождения решения модели, т.е. вычисления значений исследуемых характеристик и определение оптимальности различных вариантов изучаемого объекта с целью выбора наилучшего варианта его построения и функционирования. Данный этап представляет собой реализацию и исследование ЭММ на определенном наборе вычислительных средств. Выбор метода решения оптимизационных ЭММ зависит от математической формы, связывающей факторы модели, наличия тех или иных признаков (учет динамики, учет стохастичности и т.д.). С точки зрения корректного выбора метода решения модели наиболее существенными признаками являются характер цели исследования, формализованность связей между параметрами и характеристиками, учет вероятностной природы объекта, а также фактора времени.

По характеру цели исследования ЭММ делятся на оптимизационные(нормативные) иописательные(дескриптивные или ЭММ прямого счета).

Характерной чертой оптимизационных моделей является наличие одной или нескольких целевых функций. При этом в первом случае оптимизационные ЭММ называются монокритериальными, а во втором –многокритериальными. В общем виде монокритериальная ЭММ может быть представлена следующей системой отношений:

; (1.4)

, (1.5)

где Е– критерий оптимальности объекта;– управляемые переменные,;– неуправляемые факторы модели;;– уравнения связи, представляющие собой формализацию системы ограничений,;– целевая функция – формализованное выражение критерия оптимальности.

Выражение означает, что в ограничениях может стоять любое из приведенных в фигурных скобках логических условий.

Решение модели, заданной соотношениями (1.4) и (1.5), заключается в нахождении совокупности значений переменных

,

Обращающий в max(илиmin) целевую функциюЕпри заданных уравнениях связи.

Специфика конкретных задач управления производством определила разнообразие типов оптимизационных ЭММ. Это вызвало для ряда наиболее часто повторяющихся типов ситуаций разработку «стандартных» экономико-математических методов их описания, например, распределительные задачи различных классов, задачи управления запасами, ремонта и замены оборудования, проектирования сетей и выбора маршрутов и т.д.

Существенным признаком описательных моделей является отсутствие в них критерия оптимальности. Решение, даваемое ЭММ прямого счета, обеспечивает либо вычисление набора выходных характеристик объекта для одного или нескольких вариантов начальных условий и входных характеристик объекта, либо нахождение какой-либо совокупности значений в структурно допустимой области решений. Примеры типовых задач управления машиностроительным производством, решаемых с помощью описательных моделей, приведены в табл. 1.1.

Таблица 1.1. Примеры описательных моделей

Тип задачи	Вид модели	Математический метод решения
Задачи планирования без оптимизации (расчет объемов производства по видам продукции, увязка планов производства с ресурсами и т.п.)	Балансовые модели	Аппарат линейной алгебры, матричное исчисление
Задачи сетевого планирования и управление (СПУ) без оптимизации	Расчет по формулам модели СПУ	Аппарат теории графов
Задача учета и статистики (оперативный учет, получение различных форм отчетности и т.п.)	Расчет по формулам
Задачи контроля и анализа (анализ влияния и факторов, выявление тенденций, отслеживание отклонений и установление их причин)	Статистические модели обработки реализаций случайных величин	Факторный анализ, дисперсионный анализ, регрессионный анализ
Задача создания нормативной базы	Статистические модели обработки реализаций случайных величин	“
Расчет параметров функционирования сложных систем с неформализованными связями.	Расчет по формулам имитационных моделей	“
Задачи прогнозирования	Модели регрессионного анализа, оценка параметров и проверка статистических гипотез	Факторный анализ, дисперсионный анализ, регрессионный анализ, аппарат математической статистики

Тип задачи	Вид модели	Математический метод решения
Прочие задачи, связанные с рутинными процессами переработки информации, т.е. с расчетами по заданным формулам (расчеты подетальных спецификаций, потребности в оборудовании и производственных площадях и другие расчеты технической подготовки производства)

В зависимости от степени формализованности связей f иg_iмежду факторами моделей в выражениях (1.4) и (1.5) различаютаналитическиеиалгоритмическиемодели.

Аналитическойформой записи называется запись математической модели в виде алгебраических уравнений или неравенств, не имеющих разветвлений вычислительного процесса при определении значений любых переменных состояния модели, целевой функции и уравнений связи. Если в математических моделях единственная целевая функцияf и ограниченияg_j заданы аналитически, то подобные модели относятся к классу моделей математического программирования. Характер функциональных зависимостей, выраженных в функцияхf иg_j , может быть линейным и нелинейным. Соответственно этому ЭММ делятся налинейныеинелинейные, а среди последних в специальные классы выделяютсядробно—линейные,кусочно-линейные,квадратичныеивыпуклыемодели.

Если мы имеем дело со сложной системой, то зачастую гораздо легче построить ее модель в виде алгоритма, показывающего отношения между элементами системы в процессе ее функционирования, задаваемые обычно в виде логических условий – разветвлений хода течения процесса. Математическое описание для элементов может быть очень простым, однако взаимодействие большого количества простых по математическому описанию элементов и делает эту систему сложной. Алгоритмически же можно описывать даже такие объекты, которые в силу их сложности или громоздкости в принципе не допускают аналитического описания. В связи с этим к алгоритмическиммоделям относятся такие, в которых критерии и (или) ограничения описываются математическими конструкциями, включающими логические условия, приводящие к разветвлению вычислительного процесса. К алгоритмическим моделям относятся и так называемые имитационные модели – моделирующие алгоритмы, имитирующие поведение элементов изучаемого объекта и взаимодействие между ними в процессе функционирования.

В зависимости от того, содержит ли ЭММ случайные факторы, она может быть отнесена к классу стохастическихилидетерминированных.

В детерминированныхмоделях ни целевая функцияf , ни уравнения связиg_j не содержат случайных факторов. Следовательно, для данного множества входных значений модели на выходе может быть получен только один-единственный результат. ДлястохастическихЭММ характерно наличие среди факторовмодели, описываемой соотношениями (1.4) и (1.5), таких, которые имеют вероятностную природу и характеризуются какими-либо законами распределения, причем среди функцийf иg_j могут быть и случайные функции. Значения выходных характеристик в таких моделях могут быть предсказаны только в вероятностном смысле. Реализация стохастических ЭММ в большинстве случаев осуществляется на ЭВМ методами имитационного статистического моделирования.

Следующим признаком, по которому можно различать ЭММ, является связь с фактором времени. Модели, в которых входные факторы, а следовательно, и результаты моделирования явно зависят от времени, называются динамическими, а модели, в которых зависимость от времениtлибо отсутствует совсем, либо проявляется слабо или неявно, называютстатическими. Интересны в этом отношении имитационные модели: по механизму функционирования они являются динамическими (в модели идет имитация работы объекта в течении некоторого периода времени), а по результатам моделирования – статическими (например, ищется средняя производительность объекта за моделируемый период времени).

Статические модели представляют собой известную степень приближения к реальным объектам и системам, функционирующим во времени. Во многих случаях степень такого приближения, проявляющаяся в допущениях о неизменности или различного рода усреднениях факторов во времени (косвенно или приблизительно учитывающих фактор времени в определенных границах его изменения), является достаточной для практического применения статических моделей.

studfile.net

Что такое модель в информатике? Виды, примеры :: SYL.ru

В описываемой статье мы разберем подробно, что такое модель в информатике. Рассмотрим виды, а также способы проектирования. В данном разделе имеется множество полезных знаний, которые позволят будущим специалистам в сфере информационных технологий работать без каких-либо усилий. Для того чтобы решить любую задачу, причем неважно, научную или производственную, следует придерживаться цепочки: объект, модель, алгоритм, программа, результат, реализация. Нужно обратить внимание на второй пункт. Если этого звена не будет, то и сама проектировка не подлежит исполнению. Для чего же используется модель, и что под этим словом подразумевается? Далее раскроем этот вопрос.

Модель

Что такое модель в информатике? Благодаря ей можно составить образ какого-либо объекта, который реально существует. Также при необходимости можно отобразить все его свойства и признаки.

Для того чтобы решить какую-то задачу, следует сделать ее модель, ведь именно она и будет использоваться при дальнейшем проектировании. В школьном курсе информатики данные понятия вводятся уже в шестом классе. Однако в самом начале учат детей лишь пониманию, что же это такое.

Классификация

Описываемым термином можно назвать описание какого-либо процесса, его изображение, схему, уменьшенную копию реального объекта и так далее. Учитывая все вышеперечисленное, следует сказать, что модель — довольно широкое понятие. Его можно разделить на группы: материальное, идеальное.

Под первым типом понимают комплекс данных, который представляет собой реальный объект. Это может быть либо тело, либо процесс и так далее. Данная группа делится еще на два типа: физические, аналоговые. Эта классификация полностью условная, так как между указанными двумя подвидами нет никакой четкой черты.

Идеальную модель охарактеризовать еще труднее, потому что она связана полностью с воображением человека, его восприятием мира. К ней также можно отнести и любое произведение искусства, в том числе картины, прозу, спектакли и так далее.

Цели моделирования

Рассматривая, что такое модель в информатике, необходимо также сказать и о целях ее создания.

Моделирование — довольно важный этап, так как он позволяет осуществить большое количество задач. Именно об этом мы далее и поговорим.

Для начала, моделирование позволит человеку больше узнать о том, что его окружает. Если говорить в обширном смысле, то в самой древности люди собирали какие-то данные, информацию, факты и передавали из поколения в поколение. Примером можно назвать модель нашего мира, которая называется “глобус”. В прошлые века, как правило, моделирование было построено на несуществующих объектах, с трудом познаваемыми человеком, которые на данный момент уже имеют свою реализацию в качестве материального предмета. Большинство из них прочно закрепились в нашей жизни. Речь может идти о зонтах, мельницах и так далее.

На данный момент модели систем информатики касаются путей достижения максимального эффекта от принимаемых решений, а также обращают внимание на последствия какого-либо процесса или же действия. Если говорить о последнем подпункте, то в пример можно привести модель, которая выясняет, какие последствия будут в результате повышения стоимости проезда либо после утилизации каких-либо отходов под землей.

Задачи моделирования

Рассматривая, что такое модель в информатике, необходимо еще сказать о задачах данного способа проектирования. Описываемый процесс имеет несколько общих целей, о которых мы и поговорим далее. Если рассматривать более детально, то задачами являются этапы решения каких-либо проблем. То есть, в принципе, таковой можно назвать небольшую цель, с которой необходимо справиться, чтобы достигнуть определенных высот.

Классификация задач

При этом делятся данные задачи на две группы. Речь идет о прямых и обратных. Что касается последних, то подобные формулировки ставят перед разработчиком вопросы типа: “Как увеличить эффективность до максимума?” или “Какое же действие полностью удовлетворит имеющееся условие?” Если говорится о прямых, то такие задачи ставят перед человеком вопросы о том, что будет, если разработчик поступит так или иначе. Нужно заметить: любая прямая формулировка имеет исходные данные, а также ставит конкретные условия.

Вербальная модель

Также необходимо рассказать о видах моделей в информатике. Рассмотрим первую: вербальную. Такой метод моделирования позволяет работать с идеальными или абстрактными вопросами. Следует заметить, что в науке считаются двумя основными видами математический и информационный. Хоть и вербальный на данный момент не сильно распространен, однако он используется. Под ним подразумевают, что все задачи, цели и так далее описываются с помощью букв и связанных предложений. К таковым моделям можно отнести обычную художественную литературу, составленный протокол, какие-либо правила, информацию, описание предмета, явления и так далее.

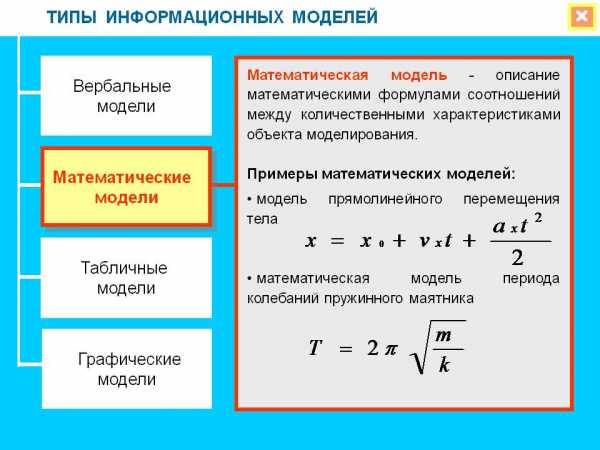
Математическая модель

Математическая модель — это в информатике один из главных видов проектирования. Она еще известна, как алгоритмическая. Следует заметить, что между математическим и информационным видами граница максимально условная. Об этом уже говорилось ранее.

Если не задаваться сложными терминами, а попытаться объяснить простым языком, то описываемая модель необходима для того, чтобы решить любую задачу или достигнуть цель при помощи математической точки зрения. Следует заметить, что каждый человек в реальной жизни занимается постоянно проектированием такой модели. Допустим, обычная бытовая задача, например, купить что-то в магазине, требует составления таковой. Человек знает, сколько стоят продукты. Необходимо посчитать, какая сумма в итоге нужна для осуществления покупки, сложив все данные. Это является обычным примером математической модели.

Информационная модель

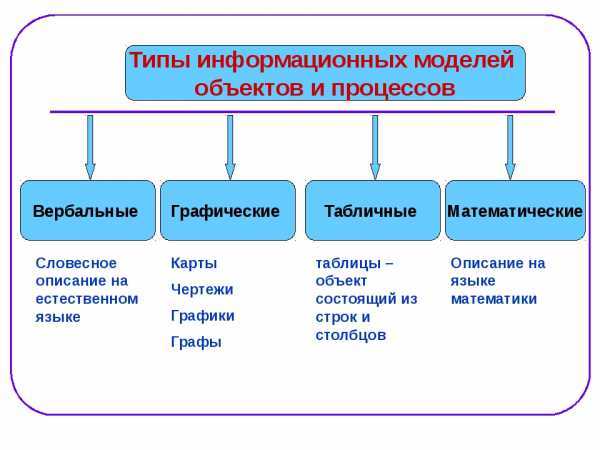
Далее рассмотрим информационную модель в информатике. Ее проектирование изучается в школе. Преподается как базовый тип.

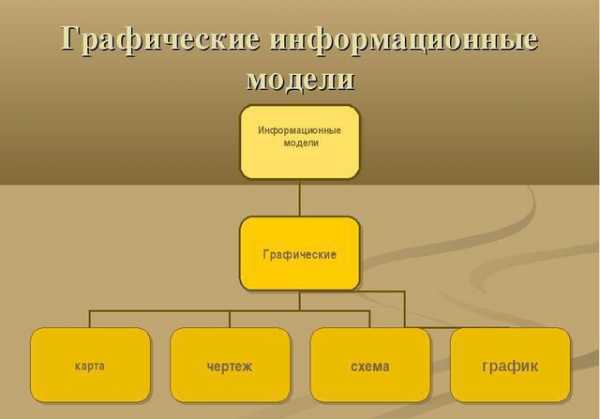
Следует заметить, что с этим видом моделирования нужно ознакомиться любому человеку, который видит свое будущее в IT-сфере. Как правило, все информационные модели создаются при помощи компьютерной техники. Причем речь идет не только конкретно о проектировании каких-то диаграмм, но используются еще и таблицы, рисунки, чертежи, схемы и так далее.

В целом информационная модель представляет собой свойства того объекта, который мы отображаем, максимально описывая его состояние, а также то, насколько он связан с окружающим миром, отношение к другим внешним предметам и влияние на них. Следует отметить, что информационной моделью может служить обычный текст, рисунок, словесное описание, чертеж, формула и так далее.

Такой вид отличается от других вышеперечисленных тем, что он является данными. То есть модель не имеет материального воплощения, так как считается примитивным комплексом информации, представленной в разном виде.

Классификацию моделей в информатике мы уже рассмотрели, теперь следует сказать о том, какой подход следует использовать, чтобы составить идеальную схему.

Необходимо понять, что такое система. Это комплекс элементов, которые взаимодействуют между собой, а также работают вместе для того, чтобы выполнить определенную задачу. Построение модели связано с использованием системного подхода. Объектом будет считаться любой комплекс, который функционирует в качестве единого в специальной среде. Иногда бывает так, что проект довольно сложный, поэтому систему делят на две части.

Цель использования

Приведем примеры моделей в информатике, для того чтобы понять, какими целями руководствуются производители при создании записи.

Следует заметить, что есть такие виды, как учебные, имитационные, игровые и так далее. Рассмотрим их.

К учебным относятся все материалы, при помощи которых осуществляется обучение.

К опытным следует добавить модели уменьшенной копии, создаваемые на основе реальных объектов.

Имитационные могут служить информацией, которая позволит понять, что произойдет в результате какого-либо действия. К примеру, если человек проводит реформу, он должен составить такую модель. Это поможет приблизительно понять то, как люди отреагируют на новые изменения. Либо же, например, чтобы человеку сделать операцию по пересадке какого-либо органа, в самом начале исследований проводится большое количество опытов. Их также можно назвать имитационной моделью. Таким образом, она представляет собой систему проб и ошибок. Это позволяет принимать более оправданные решения.

Игровой моделью является система, которая ставит определенные объекты в какие-либо рамки. Это может быть экономическая, деловая или военная игра. Таким образом, человек способен понять поведение определенного объекта в нужной ему среде.

Научно-техническую следует использовать для того, чтобы изучить какое-либо явление и процесс, который трудно исследовать в обычной жизни. Это может быть создание прибора, имитирующий грозовой разряд, либо же модель движения, полностью копирующая солнечную систему.

Способ представления

Подытоживая все вышесказанное о моделях данных в информатике, необходимо разузнать, как же представляется созданная запись.

Она бывает материальная и нематериальная. К первому виду нужно отнести все копии, которые были сняты с существующих объектов. Таким образом, их можно взять в руки, потрогать, понюхать и так далее. Они даже способны имитировать какие-либо свойства оригинального объекта, а также его действия. Данные материальные модели являются опытным методом проектирования.

К нематериальным относятся те, которые работают на теории. Они идеальные либо же абстрактные. Эта категория также имеет несколько типов. Речь идет об информационных, а еще воображаемых вариантах. Первый представляет собой перечень данных, который касается определенного объекта. Таковыми можно назвать таблицы, рисунки, схемы и так далее.

Однако многих их интересует, почему же данная модель класса информатики считается нематериальной. Текст хоть и напечатан, таблица составлена, но его потрогать нельзя. Именно поэтому данная модель является абстрактной. К слову, среди информационных вариантов записи имеются наглядные примеры.

К воображаемой модели относят то, что называется творческим процессом, то есть все происходящее в сознании человека. Это побуждает его создать на основе данной схемы оригинальный объект.

www.syl.ru

модель — это… Что такое модель?

МОДЕ́ЛЬ [дэ́], -и; ж. [франц. modèle]

1. Образец какого-л. нового изделия, служащий наглядным примером для кого-, чего-л. Последние модели обуви. Выставка моделей детской одежды.

2. Образец, с которого снимается форма для отливки или для воспроизведения в другом материале.

3. Тип, марка, образец конструкции. Новые модели телевизоров. Жигули первой модели.

4. Предмет, точно воспроизводящий в уменьшенном виде или в натуральную величину какой-л. другой предмет. М. корабля. Сделать из спичек м. телебашни. Собрать м. самолёта.

5. Схема, математическое описание устройства какого-л. физического объекта или процесса, протекающего где-л. (обычно невидимого). М. атома, головного мозга. М. крекинга нефти. М. управления производством.

6. То, что служит натурой для художественного воспроизведения. М. для рисунка. Моделью для наброска послужил бюст Бетховена. Живая м. // Тот, кто позирует перед художником; натурщик, натурщица. Обнажённая м. Придать модели нужную позу.

◁ Моде́льный (см.).

* * *

моде́ль (франц. modèle, от лат. modulus — мера, образец), 1) образец (эталон, стандарт) для массового изготовления какого-либо изделия или конструкции; тип, марка изделия. 2) Изделие (из легкообрабатываемого материала), с которого снимается форма для воспроизведения (например, посредством литья) в другом материале; разновидности таких моделей — лекала, шаблоны, плазы. 3) Позирующий художнику натурщик или изображаемые предметы («натура»). 4) Устройство, воспроизводящее, имитирующее строение и действие какого-либо другого («моделируемого») устройства в научных, производственных (при испытаниях) или спортивных (см. Моделизм спортивный) целях. 5) В широком смысле — любой образ, аналог (мысленный или условный: изображение, описание, схема, чертёж, график, план, карта и т. п.) какого-либо объекта, процесса или явления («оригинала» данной модели), используемый в качестве его «заместителя», «представителя» (см. Моделирование). 6) В математике и логике моделью какой-либо системы аксиом называют любую совокупность (абстрактных) объектов, свойства которых и отношения между которыми удовлетворяют данным аксиомам, служащим тем самым совместным (неявным) определением такой совокупности. 7) Модель в языкознании — абстрактное понятие эталона или образца какой-либо системы (фонологической, грамматической и т. п.), представление самых общих характеристик какого-либо языкового явления; общая схема описания системы языка или какой-либо его подсистемы.

* * *

МОДЕЛЬ МОДЕ́ЛЬ (лат. modulus — мера, образец),
1) образец (эталон, стандарт) для массового изготовления какого-либо изделия или конструкции; тип, марка изделия.
2) Изделие (из легкообрабатываемого материала), с которого снимается форма для воспроизведения (напр., посредством литья) в другом материале; разновидности таких моделей — лекала, шаблоны, плазы.
3) Позирующий художнику натурщик или изображаемые предметы («натура»).
4) Устройство, воспроизводящее, имитирующее строение и действие какого-либо др. («моделируемого») устройства в научных, производственных (при испытаниях) или спортивных (см. Моделизм спортивный (см. МОДЕЛИЗМ СПОРТИВНЫЙ)) целях.
5) В широком смысле — любой образ, аналог (мысленный или условный: изображение, описание, схема, чертеж, график, план, карта и т. п.) какого-либо объекта, процесса или явления («оригинала» данной модели), используемый в качестве его «заместителя», «представителя» (см. Моделирование (см. МОДЕЛИРОВАНИЕ)).
6) В математике и логике — моделью какой-либо системы аксиом называют любую совокупность (абстрактных) объектов, свойства которых и отношения между которыми удовлетворяют данным аксиомам, служащим тем самым совместным (неявным) определением такой совокупности.
7) Модель в языкознании — абстрактное понятие эталона или образца какой-либо системы (фонологической, грамматической и т. п.), представление самых общих характеристик какого-либо языкового явления; общая схема описания системы языка или какой-либо его подсистемы.

Энциклопедический словарь. 2009.

dic.academic.ru

Информационная модель — Википедия

Материал из Википедии — свободной энциклопедии

Пример информационной модели.

Информационная модель — модель объекта, представленная в виде информации, описывающей существенные для данного рассмотрения параметры и переменные величины объекта, связи между ними, входы и выходы объекта и позволяющая путём подачи на модель информации об изменениях входных величин моделировать возможные состояния объекта^[1].

Информационная модель (в широком, общенаучном смысле) — совокупность информации, характеризующая существенные свойства и состояния объекта, процесса, явления, а также взаимосвязь с внешним миром.

С. А. Терехов^[кто?] выделяет несколько типов информационных моделей, отличающихся по характеру запросов к ним^[2]:

1. Моделирование отклика системы на внешнее воздействие
2. Классификация внутренних состояний системы
3. Прогноз динамики изменения системы
4. Оценка полноты описания системы и сравнительная информационная значимость параметров системы
5. Оптимизация параметров системы по отношению к заданной функции ценности
6. Адаптивное управление системой

Информационные модели в информатике[править | править код]

Информационная модель в информатике — это представление понятий, связей, ограничений, правил и операций, предназначенное для определения семантики данных для конкретной проблемной области^[3].

Информационное моделирование здания — это подход к возведению, оснащению, обеспечению эксплуатации и ремонту здания (к управлению жизненным циклом объекта), который предполагает сбор и комплексную обработку в процессе проектирования всей архитектурно-конструкторской, технологической, экономической и иной информации о здании со всеми её взаимосвязями и зависимостями, когда здание и все, что имеет к нему отношение, рассматриваются как единый объект^{[источник не указан 1030 дней]}.

Процесс коллективного создания и использования информации о сооружении формирует основу для всех решений на протяжении жизненного цикла объекта (от самых ранних концепций до рабочего проектирования, строительства, эксплуатации и сноса).

• Терехов С. А. Нейросетевые информационные модели сложных инженерных систем // Нейроинформатика / А. Н. Горбань, В. Л. Дунин-Барковский, А. Н. Кирдин и др.. — Новосибирск: Наука. Сибирское предприятие РАН, 1998. — 296 с.

Serov N.V.:

• The Ontology of Dimensionality for Anthropological Database Modeling. // Automatic Documentation and Mathematical Linguistics, 2010, Vol. 44, No. 1, pp. 1-15 [1];
• Ibid.Idem.2016, Volume 50, Issue 3, pp 91-103, An information model of light quantization [2].

ru.wikipedia.org

No related posts.