Сложный план примеры: Сложный план текста – пример — Заработок в сети Интернет. Как заработать на дому в Интернете. Удаленная работа в сети.

Содержание

как составить сложный план? — Школьные Знания.com

Выпиши из предложений и распредели по колонкам глаголы, вставляя пропущенные гласные в окончаниях. Слова записывай в той форме, в какой они даны в пре … дложениях (если при глаголе есть частица не, то запиши частицу и глагол через пробел). 1. Собака куса__т меня за пятки. 2. Издали — золото, приблиз__шься — медь. 3. Братья кол__т дрова. 4. По краям росписи мастер нанос__т кружевной золотой орнамент. срочно пожалуйста

выписать краткое прилог подчеркнуть как член предложения

Сколько членов предложения в предложении «Я хотел непременно съездить в какую-нибудь деревенскую глушь.»

Расставьте запятые. Такую маленькую мышку как я быстро съедят.

на следующий день он обнаружил своей отаре незнакомого белого ягненка синтаксический разбор

Напишите о сильных и слабых сторонах, возможностях и угрозах восстания 1817 года.

Задание 2 Прочитайте предложения и составьте новые, которые должны начинаться с заданных слов и передавать смысл исходных предложений, следуя образцу … .

Дополнительно присваивается 5 баллов за качество языка. Образец: Я считаю, что культуру определяет время и общество. Время и общество, по моему мнению, ………………………………………[1] Ответ: Время и общество, по моему мнению, определяют культуру. 1.История бразильского карнавала началась в период колонизации Южной Америки европейцами в 17 веке. В 17 веке……………………………..……………………………………………. …………………………………………………………………………………………………………….[1] 2. Вскоре этот праздник был запрещен по причине многочисленных жалоб граждан. По причине многочисленных жалоб………..……………………………………….[1] 3. Например, один из костюмированных балов с европейскими танцами был проведен в 1840 году в одном из крупнейших отелей Рио-де-Жанейро. В 1840 году …………………………………………….………………………….[1] 4. Основателем современного бразильского карнавала можно считать сапожника Жозе Ногейра де Асеведо Паредес. Сапожник Жозе Ногейра де Асеведо Паредес………………………………… ………………………………………………………………………………….

. [1] 5. В 1852 году в один из дней карнавала он вышел на улицу, собрав множество друзей и взяв с собой ударные инструменты. В один из дней карнавала………………………………………………………. …………………………………………………………………………………………………………………………………………………………………………………………………………[1] 6. Два десятилетия спустя в Бразилию прибыло множество африканцев, которые когда-то работали на кофейных плантациях. Два десятилетия спустя в Бразилию прибыло множество африканцев,……… ……………………………………………………………………………………… ………………………………………………………………………………………………………………..[1] 7. Группы мужчин и женщин прошлись по улицам с зажигательными танцами, а после в бразильских карнавалах появились африканские мотивы. Африканские мотивы…………………………………………………………………………………… ……………………………………………………..

…………………………………………………………[1] 8. В конце 1880-х появилась первая песня-марш, созданная специально для бразильского карнавала. В конце 80-х годов ……….……………………………………………………… ……………………………………………………………………………………[1] 9. Марш, написанный в веселом, жизнерадостном темпе, задавал ритм движения танцующих. Марш веселого…………………………………………………………………… ……………………………………………………………………………………[1] 10. Первое формальное карнавальное шествие прошло в 1935 году на известной бразильской площади 11 июня. В 1935 году на………………………………………………………………….…. ………………………………

Найдите грамматическую основу и все члены предложения: Сейчас это слово для нас простой знак вежливости

В старом саду «дорожки» заросли вьюном. Яблоня покрылась красными «шариками» плодов. Около бочки с дождевой водой поселились лягушки. Сад наполнился н … ежным ароматом фруктов и овощей .К бабушке в деревню приехали внуки. Они дружно принялись за работу. От яблони к яблони. прорыли канавку. Теплая вода напоила деревья. Они расправили нежно листочки, засверкали на ярком солнышке яблочки. Цветы напеолнили воздух ароматом. Вечером в саду под липой собралась вся семья. Хорошо пить чай в саду! 1. Вставьте пропущенные буквы. 2. Прочитайте текст. 3. Озаглавьте текст. 4. Найдите в тексте опрелеления. 5. Разберите по составу выделенные слова.

Прочитайте отрывок из письма. Кто и кому написал его? К каким письмам вы отнесли бы его: деловым или дружеским? Какие чувства выражены в нём? Мой милы … й друг, прошу тебя ответить как можно скорее на это письмо… Я услышал от твоего брата и от твоей матери, что ты болен: правда ли это? Скорее, скорее ответь.

Как составить сложный план текста

Понятие сложного плана

План представляет собой логически связанный, последовательный перечь основных мыслей автора. Систематизация текстового материала не только облегчает запоминание, работу с ним, но и помогает уяснить смысл и цель написания, выделить основные мысли, вкладываемые в текст автором.

Основные требования к сложному плану:

структурированность – план должен соответствовать структуре текста, иметь начало и заключение;
грамотная формулировка мыслей — название пунктов и подпунктов должны отражать или дополнять основную тему, не наслаиваться и не дублировать друг друга;
информативность – название должны содержать необходимую информацию для последующего воспроизведения, не быть слишком общими;
последовательность – каждый пункт или подпункт следует из предыдущего, не нарушая логику и целостность изложения мыслей.

Порядок составления сложного плана

При составлении сложного плана необходимо обращать внимание на абзацы и наиболее яркие образы, описываемые автором – акцентирование внимание на них способствует облегчению процесса выполнения данной работы:

прочитать текст, выявить главную тему;
выделить основные смысловые текстовые части и озаглавить их – они станут пунктами плана;
среди крупных смысловых частей выделить мысли, вкладываемые автором, и также озаглавить их – это подпункты. В каждом пункте должно присутствовать минимум два подпункта;

проверить формулировку названий пунктов и подпунктов – они должны быть не отрывками из предложений, а заголовками, сформулированными самостоятельно для смысловых частей текстового материала;
проверить, раскрывает ли план основную мысль текста и отображает ли его структуру.

Например, один из вариантов плана по теме «Феодальная раздробленность Руси»:
1.Причины появления феодальной раздробленности;
а) социально – экономические причины;
б) политические причины.
2. Развитие Руси в период раздробленности;
а) специфика развития русских княжеств;
б) культура периода раздробленности;
в) борьба с иноземными захватчиками.
3. Последствия феодальной раздробленности.

Сложный план текста — структура, план и пример составления

Мамонты и тексты — общие моменты

План текста — как скелет, по которому учёные могут восстановить строение тела доисторического животного. Так и читатель по плану текста перед чтением может понять его структуру, а после — вспомнить его содержание. Достигается этот эффект за счёт того, что каждый пункт плана описывается словами, максимально полно раскрывающими содержательную часть абзаца, к которому они относятся.

А каждый такой абзац или параграф, если абзацев несколько, характеризуется логической завершённостью.

Два уровня сложности

В зависимости от того, насколько подробно описывается предмет письменного материала, его план может быть или простым, или сложным.

Простой характеризуется одноуровневой конструкцией, которая содержит не менее двух, но не более пяти пунктов и подходит для схематизации коротких сообщений или небольших рассказов.

Заголовки простой структуры, как правило, описываются с помощью существительных и зависимых слов — других существительных, прилагательных и глаголов.

Пример простого плана на тему «Сказки о рыбаке и рыбке» А. С. Пушкина:

Старик, старуха и Золотая Рыбка.
Три желания старухи.
Последний каприз царицы.
Старик, старуха и разбитое корыто.

Сложный план характеризуется многоуровневой конструкцией, которая может содержать от пяти и более пунктов; каждый пункт может содержать подпункты; последних должно быть не менее двух в одном пункте. Для составления многоуровневой конструкции используется принцип матрёшки — с помощью иерархической схемы наглядно демонстрируется главная идея текста и её составные части.

Сложный план подходит для написания материалов с глубоким уровнем детализации, например, для произведений художественной литературы.

Хрестоматийный для русского языка пример на тему уже знакомой сказки А. С. Пушкина:

Введение.
Бедная жизнь старика со старушкой.

Кого поймал рыбак?
Почему дед отпустил свой улов?
Что изменило жизнь стариков?

Недовольство старухи.

Что должен был сделать старик?
Кем хотела стать жадная бабка?

Исчезновение волшебной рыбки.
Старик, его жена и разбитое корыто.
Заключение

Как правильно составить план текста

Для того чтобы грамотно написать план, например, классного сочинения, автор должен хорошо владеть предметом, о котором он собирается писать.

В качестве источника информации автор может опираться или на собственный опыт, или на чужой; в последнем случае автору нужно много читать на заданную тему.

Вне зависимости от источника информации, её следует:

Изложить в письменном виде;
Разделить на абзацы, которые представляют собой самостоятельные смысловые блоки;
Задать к каждому блоку вопрос — о чём собственно идёт речь?
Перефразировать вопросительное предложение в утвердительное и таким образом придумать для каждого смыслового блока название, отражающее его содержание.

Идеально составленный план при одном взгляде на него должен восстановить в памяти читателя подробное содержание текста любой сложности.

Четыре критерия оценки

План теста должен соответствовать четырём критериям, предназначение которых — помогать авторам как школьных сочинений, так и основательных литературных произведений адекватно оценивать свои работы:

Первый из критериев — это структурность — она делит тело, например, газетной статьи на абзацы. Последовательная или иерархическая структура абзацев предполагает, что и текст, и его план по структуре совпадают.
Второй критерий — это ясность формулировки, она предполагает, что названия заголовков выражают законченные мысли.
Третий критерий — информативность, она позволяет читателю логически ориентироваться в расположении смысловых блоков текста.
Четвёртый критерий — это последовательность, которая предполагает, что заголовки и подзаголовки не только названы таким образом, чтобы раскрыть их содержательную часть, но и расположены в такой последовательности, которая отражает внутреннюю (художественную, историческую или научную) логику развития сюжета истории целиком.

Пять видов названия рубрик

Заголовок и подзаголовки представляют собой названия пунктов и подпунктов плана. В зависимости от стилистической принадлежности письменного материала, а также от его детализации названия пунктов бывают пяти видов:

Вопросные — они состоят из вопросительных слов (кто, что, зачем, почему), ответ на которые содержится в информативной части абзаца. Такие заголовки подходят для коротких новостных статей.
Тезисные (они же назывные) — в виде кратко сформулированных мыслей, они выражают смысл блока, к которым относятся. Для тезисных заголовков используются максимум существительных и прилагательных и минимум глаголов.
Цитатные — они представляют собой дословные высказывания из абзацев. Это, как правило, цитаты, раскрывающие основные мысли информационных блоков.
План — опорная схема — это такие заголовки, которые содержат ключевые слова, описывающие смысловые значения абзацев.
Смешанные названия заголовков — они могут содержать виды разных способов описания заголовков. Названия смысловых блоков смешанного плана помогают структурировать текст по уровням: чем больше деталей, тем больше уровней. Заголовки одного уровня могут принадлежать только одному из предыдущих четырёх видов названий.

Использовать смешанные названия можно в качестве рабочей версии, которую в процессе работы над письменным материалом можно редактировать — добавлять и удалять рубрики, и видоизменять их.

Смешанные названия также позволяют автору развернуть перед внутренним взором читателя всю глубину своего письменного шедевра.

Три функции заголовков

План письменного материала состоит из пунктов или рубрик, которым присвоены названия — заголовки, слова для описания которых должны быть подобраны таким образом, чтобы выполнять следующие функции:

Организовывать и направлять внимание читателя;
Раскрывать структуру текста — определять относительное значение заголовков и подзаголовков, а также место каждого из последних в общей структуре письменного материала;
Выполнять функцию справочной карты, с помощью которой в теле, например, лекции ученик должен легко находить искомые смысловые блоки.

Чем логичнее структура текста, и чем точнее названия заголовков, тем автору легче управлять вниманием читателя, а последнему — следить за мыслью автора. Какой сложности выбрать план, зависит от того:

Следуют ли мысли письменного изложенная одна за другой, без иерархической подчинённости — последовательно;
Или мысли (в широком смысле — информация) представляют собой составные части одной главной мысли — идейной доминанты текста.

Два типа плана, четыре критерия его оценки на предмет соответствия некоторому идеалу, пять видов заголовков и три функции последних — всё это предназначено, с одной стороны, помогать авторам отделять в теле своих рассказов главное от второстепенного — грамотно составлять планы текстов; а с другой стороны — помогать читателям ориентироваться в изложенной информации и понимать то, о чём пишется.

СЛОЖНЫЙ ПЛАН ГОТОВОГО ТЕКСТА — ТЕКСТ — РЕЧЬ — Русский язык 6 клас — Е.

И. Быкова — Освіта 2014 рік

РЕЧЬ

ТЕКСТ

§ 52. СЛОЖНЫЙ ПЛАН ГОТОВОГО ТЕКСТА.

Подробный устный пересказ научно-популярного текста по сложному плану

327. Прочитайте и сравните две памятки по написанию простого и сложного планов текста. По результатам сравнения определите, чем отличается сложный план от простого.

Памятка по составлению простого плана	Памятка по составлению сложного плана
1. Прочитайте текст.	1. Прочитайте текст.
2. Разделите текст на смысловые части и выделите в каждой из них основную мысль.	2. Разделите текст на основные смысловые части и озаглавьте их (пункты плана).
3. Озаглавьте каждую часть.	3. Разделите на смысловые части содержание каждого пункта и озаглавьте их (подпункты плана).
4. Просмотрите текст, проверяя, все ли главные мысли вы выделили и отразили в плане.	4. Просмотрите текст, проверяя, полностью ли в плане отражено основное содержание.
5. Запишите план.	5. Запишите план.

— Сложный план, как и текст, состоит из трёх частей: вступления, основной части и заключения. Он более полно отражает содержание и даёт читателю ясное представление о логике и композиции текста.

Сложный план отличается от простого тем, что отдельные его пункты, являющиеся заглавиями значительных частей текста, включают в себя подпункты (т. е. заголовки более мелких частей), в которых тема раскрывается более детально.

328. I. Прочитайте текст. Докажите, что он является связным и цельным.

Мой знакомый вместе со своими товарищами-инженерами занимается проблемами машинного зрения. В поисках подходящих глаз для роботов они изучали глаза разных живых существ, их строение, достоинства и недостатки. Были исследованы глаза лягушки, затем — кошки, голубя, человека. Каждый раз открывались удивительные вещи.

Выяснилось, например, что, вопреки всеобщему мнению, кошка видит в темноте немногим лучше, чем мы с вами. А голубь может рассмотреть зёрнышко пшеницы за несколько сот метров, замечает разницу в величине шариков, даже если она составляет сотые доли миллиметра!

Больше всего поразил исследователей глаз человека. Главная его часть — сетчатка — состоит из множества светочувствительных элементов — палочек и колбочек. Палочки воспринимают чёрно-белое изображение, колбочки — цветное. Они настолько малы, что на участке сетчатки, равном по своим размерам точке на этой странице, размещается двадцать тысяч палочек и колбочек.

Сколь же трудной была задача инженеров — создать устройство, которое могло бы соперничать с человеческим глазом! Тем не менее, такой прибор был сконструирован — это телевизионная камера.

(С. Зигуненко)

II. Определите, из каких смысловых частей состоит текст. Озаглавьте их и составьте простой план, запишите его.

III. Найдите средства связи между предложениями первого абзаца.

IV. Объясните значение слов робот, инженер. Проверьте себя по словарю.

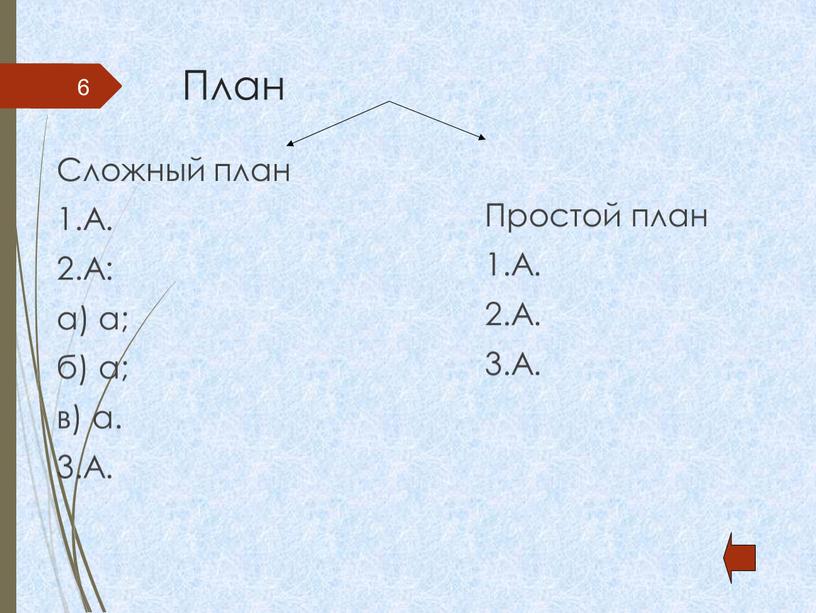
329. I. Рассмотрите схему сложного плана. Расскажите, как пунктуационно оформляется сложный план.

Схема сложного плана текст

I. Вступление.

II. Основная часть (развитие действия).

2. …

3. …

…

III. Заключение.

II. Сравните данный на с. 218 сложный план сочинения по теме «Почему книгу называют другом» с простым планом, составленным вами к тексту предыдущего упражнения.

Почему книгу называют другом

План

I. «Книга — лучший друг» (Пословица).

II. Почему книгу называют другом.

1. «…Книга учит людей хорошему» (Н. Носов).

2. Книга — источник знаний.

3. Книга — наша помощница.

4. «Книга в счастье украшает, а в несчастье утешает» (Пословица).

III. Книгу надо беречь, как друга.

330. I. Определите структурные части (вступление, основную часть, заключение) в тексте из упр. 328.

II. Определите и сформулируйте кратко, о чём говорится в основной части. Запишите эти краткие формулировки.

III. Используя памятку и теоретический материал, составьте сложный план текста упр. 328.

IV. Устно перескажите содержание текста в соответствии с составленным сложным планом.

ПопередняЗмістНаступна

Відвідайте наш новий сайт — Матеріали для Нової української школи — планування, розробки уроків, дидактичні та методичні матеріали, підручники та зошити

ЕГЭ по обществознанию. Задание 28. План

№	Критерии оценивания ответа на задание 28	Баллы
28. 1	*Раскрытие темы по существу*	3
	Сложный план содержит не менее трёх пунктов, включая два пункта, наличие которых позволит раскрыть данную тему по существу. Оба этих «обязательных» пункта детализированы в подпунктах, позволяющих раскрыть данную тему по существу	3
	Сложный план содержит не менее трёх пунктов, включая два пункта, наличие которых позволит раскрыть данную тему по существу. Только один из этих «обязательных» пунктов детализирован в подпунктах, позволяющих раскрыть данную тему по существу	2
	Сложный план содержит не менее трёх пунктов, включая только один пункт, наличие которого позволит раскрыть данную тему по существу. Этот «обязательный» пункт детализирован в подпунктах, позволяющих раскрыть данную тему по существу	1
	Все иные ситуации, не предусмотренные правилами выставления 2 и 1 балла. ИЛИ Случаи, когда ответ выпускника по форме не соответствует требованию задания (например, не оформлен в виде плана с выделением пунктов и подпунктов)	0
	Указания по оцениванию: 1. Пункты/подпункты, имеющие абстрактно-формальный характер и не отражающие специфики темы, не засчитываются при оценивании. *2. Если по критерию 28.1 выставляется 0 баллов, то по критерию 28.2 выставляется 0 баллов*
28.2	*Корректность формулировок пунктов и подпунктов плана*	1
	Формулировки пунктов и подпунктов плана корректны и не содержат ошибок, неточностей	1
	Все иные ситуации	0
	Максимальный балл	4

Онлайн тест по Русскому языку по теме Сложный план текста

Тест по теме «сложный план текста» создан, чтобы проверить, как усвоился материал по работе с материалом. Обычно сложный перечень требуется либо для пересказа статьи или главы, либо для упрощения запоминания какой-то информации. На его основе очень удобно рисовать схемы и таблицы.

В 7 классе в школах дети начинают более углубленно изучать литературные произведения, делить его на смысловые части для упрощения восприятия материала. Так что этот тест сможет осилить любой человек, начиная с возраста семиклассника. Чтобы успешно ответить на вопросы, нет необходимости зубрить какие-то книги, можно просто вникнуть в тему. Непосредственно перед началом тестирования есть ссылка на сайт, где в хорошо организованной форме размещена вся информация по исследуемой теме.

Для его успешного прохождения необходимо знать, что такое план. Напомню, что это перечень мыслей, высказанных автором.Также перед опросником стоит вспомнить о последовательности критериев, соответствующих плану, содержащему не только пункты, но и подпункты: структурированность, грамотная формулировка, информированность и последовательность.

И наконец обратите внимание на этапы по составлению сложного перечня. Помните, что сначала всегда читаем текст и выделяем в нем основную мысль, а уже затем только делим его на смысловые части. Если дан небольшой текст, то ей обычно является абзац. Далее формируются пункты и подпункты для каждой выделенной части. Но не надо забывать про проверку. Составление сложного плана текста – это простая математика. Есть конкретная очередность действий, по завершении которых итоговый план будет готов.

Пройти тест онлайн

Может быть интересно

Ещё никто не оставил комментария, вы будете первым.

Написать комментарий
Спасибо за комментарий, он будет опубликован после проверки
21 Примерный образец сложного плана контрольной работы
IХ. Примерный образец сложного плана контрольной работы
Тема: БИОЭТИКА
Сложный план
I.        Актуальность исследования проблем биоэтики.
II.     Основная часть. Биоэтика:
1.      Этика жизни или биоэтика.
2.      Этика жизни и традиции русской философии.
3.      Биоэтика и традиции современной американской культуры.
4.      Модели моральной медицины в современном американском обществе.
а) Модель технического типа.
б) Модель сакрального типа.
в) Модель коллегиального типа.
г) Модель контрактного типа.
5.      Принцип информированного согласия.
6.      Биоэтика и психиатрия.
III.   Заключение и выводы по рассматриваемой проблеме.

Примеры оформления библиографического описания списка источников, используемых в контрольной работе
Характеристика оформления            Пример
Источник
Монография       Флурнуа Т. Принципы религиозной психологии. – К., (один, два или      1913. – С.87.
три автора)
Многотомные      Ницше Ф. Так говорил Заратустра // Соч.: В 2 т. – М.,
издания                1990. – Т.2.
Переведенные   Религиозные традиции мира. В 2 т. // Пер. с англ. – М.,
издания              1966. – Т.1: Христианство. – 576 с.
Учебное                Релігієзнавство: Підручник / За ред.. В.І. Лубського,
пособие                   В.І. Теремка. – К., 2000. – 302 с.
Энциклопедии           Народы и религии мира: Энциклопедия // Гл. ред.
            В.А.Тишков. Редкол.: О.Ю.Артемова, С.А.Арутюнов
            и др. – М., 1999. – С.928.
Словари            Христианство: Энциклопед. Словарь: В 2 т. / Ред. Кол.:
          С.С. Аверинцев и др. – М., 1993. – 863 с.
Составляющие               Николай Кузанский. О мире веры // Вопросы
части из журнала           философии. – 1992. – №5.
Сложный самолет
Нет, , а не , эта комплексная плоскость …
… это комплексная плоскость :
A самолет для комплексных номеров !
(Также называется «диаграммой Аргана»)
Реальное и воображаемое составляют комплекс
Комплексное число — это комбинация действительного и мнимого числа:
Реальный номер — это тип номера, который мы используем каждый день.
Примеры: 12,38, ½, 0, −2000
Когда мы возводим в квадрат действительное число, мы получаем положительный (или нулевой) результат:
2 ² = 2 × 2 = 4
1 ² = 1 × 1 = 1
0 ² = 0 × 0 = 0
Что мы можем возвести в квадрат, чтобы получить −1?
? ² = -1
Возведение в квадрат −1 не работает, потому что умножение отрицательных чисел дает положительное значение: (−1) × (−1) = +1, и никакое другое действительное число также не работает.
Значит математика кажется неполной …
… но мы можем заполнить пробел на , представив , есть число, которое при умножении на само себя дает −1
(назовем его i для мнимого):
и ² = -1
И вместе:
Комплексное число — это комбинация действительного и мнимого числа
Примеры: 3,6 + 4 i , −0,02 + 1,2 i , 25-0.3 i , 0 + 2 i
Отображение комплексного числа на плоскости
Возможно, вам знакома числовая строка:
Но где мы помещаем комплексное число вроде 3 + 4 i ?
Пусть линия вещественных чисел идет влево-вправо, как обычно, а линия мнимых чисел идет вверх и вниз :
Затем мы можем построить комплексное число, например 3 + 4i :
3 единицы вдоль (действительная ось),
и 4 единицы вверх (мнимая ось).
А вот 4 — 2i :
4 единицы по (действительная ось),
и на 2 единицы вниз (мнимая ось).
А это комплексная плоскость :
комплексный , потому что это комбинация действительного и мнимого,
плоскость потому что она похожа на геометрическую плоскость (2-х мерную).
Весь новый мир
Теперь давайте перенесем идею о плоскости (декартовы координаты, полярные координаты, векторы и т. Д.) В комплексные числа.
Он откроет совершенно новый мир чисел, более полных и элегантных, как вы увидите.
Комплексное число как вектор
Мы можем думать о комплексном числе как о векторе.

Это вектор.
Имеет величину (длину) и направление.
А вот и комплексное число 3 + 4i
как вектор :
Добавление
Вы также можете складывать комплексные числа как векторы:
Чтобы сложить комплексные числа 3 + 5i и 4 — 3i :
сложите действительные числа и
сложите мнимые числа
отдельно, вот так:
(3 + 5 i ) + (4 — 3 i ) = (3 + 4) + (5 — 3) i
= 7 + 2 и
Полярная форма
Давайте снова воспользуемся 3 + 4i :
Вот в полярной форме:
Таким образом, комплексное число 3 + 4i также может отображаться как расстояние (5) и угол (0. 927 радиан).
Давайте посмотрим, как преобразовать из одной формы в другую, используя преобразование из декартовой системы координат в полярную:
Пример: номер
3 + 4i
из 3 + 4i :
r = √ (x ² + y ²) = √ (3 ² + 4 ²) = √25 = 5
θ = tan ^-1 (y / x) = tan ^-1 (4/3) = 0,927 (до 3 десятичных знаков)
И получаем расстояние (5) и угол (0.927 радиан)
Снова:
x = r × cos ( θ ) = 5 × cos (0,927) = 5 × 0,6002 … = 3 (достаточно близко)
y = r × sin ( θ ) = 5 × sin (0,927) = 5 × 0,7998 … = 4 (достаточно близко)
И расстояние 5 и угол 0,927 снова становятся 3 и 4
На самом деле, обычный способ записать комплексное число в полярной форме — это
.
x + i y = r cos θ + i r sin θ
= r (cos θ + i sin θ )
И «cos θ + i sin θ » часто сокращается до «cis θ », поэтому:
x + iy = r цис θ
cis — это просто сокращение для cos θ + i sin θ
Итак, мы можем написать:
3 + 4i = 5 цис 0. 927
В некоторых предметах, например, в электронике, «цис» используется очень много!
Сводка
Комплексная плоскость — это плоскость, на которой:
действительные числа слева направо и
мнимых числа, бегущих вверх-вниз.
Чтобы преобразовать из декартовой в полярную форму:
r = √ (x ² + y ²)
θ = tan ^-1 (y / x)
Чтобы преобразовать из полярной в декартову форму:
x = r × cos ( θ )
y = r × sin ( θ )
Полярная форма r cos θ + i r sin θ часто сокращается до r cis θ
Далее… узнать об умножении комплексных чисел.
Нанести комплексные числа на комплексную плоскость
Мы не можем нанести комплексные числа на числовую линию, как действительные числа. Однако мы все еще можем изобразить их графически. Чтобы представить комплексное число, нам нужно обратиться к двум компонентам числа. Мы используем комплексную плоскость , которая представляет собой систему координат, в которой горизонтальная ось представляет реальный компонент, а вертикальная ось представляет мнимый компонент.Комплексные числа — это точки на плоскости, выраженные в виде упорядоченных пар ( a , b ), где a представляет координату для горизонтальной оси, а b представляет координату для вертикальной оси.
Рисунок 2
Рассмотрим число [латекс] -2 + 3i \\ [/ latex]. Действительная часть комплексного числа –2, а мнимая часть — 3 i . Мы строим упорядоченную пару [латекс] \ left (-2,3 \ right) \\ [/ latex], чтобы представить комплексное число [latex] -2 + 3i \\ [/ latex] .
Общее примечание: сложная плоскость
Рисунок 3
В комплексной плоскости горизонтальная ось является действительной осью, а вертикальная ось — мнимой осью .
Как: дано комплексное число, изобразите его компоненты на комплексной плоскости.
Определите действительную и мнимую части комплексного числа.
Переместитесь по горизонтальной оси, чтобы показать действительную часть числа.
Двигайтесь параллельно вертикальной оси, чтобы показать мнимую часть числа.
Обозначьте точку.
Пример 2: Построение комплексного числа на комплексной плоскости
Постройте комплексное число [латекс] 3 — 4i \ [/ латекс] на комплексной плоскости.
Решение
Действительная часть комплексного числа равна 3, а мнимая часть — –4 i . Строим упорядоченную пару [латекс] \ left (3, -4 \ right) \\ [/ latex].
Рисунок 4
Попробуй 2
Постройте комплексное число [latex] -4-i \\ [/ latex] на комплексной плоскости.
Решение
Культурных центров: 50 примеров в плане и в разрезе
Культурные центры: 50 примеров в плане и в разрезе
Cortesía de Fabián Dejtiar ПоделитьсяПоделиться
Facebook
Twitter
Pinterest
Whatsapp
Почта
Или
https://www. archdaily.com/
6/cultural-centers-50-examples-in-plan-and-section
Сколько раз вы сталкивались с проблема проектирования культурного центра? Хотя это может показаться настоящим подвигом, многим архитекторам пришлось разработать программу, сочетающую общественный центр с культурой.
Среди проектов, опубликованных на нашем сайте, мы нашли множество примеров, которые подчеркивают различные ответы, от гибких конфигураций до сайтов, которые отдают приоритет центральным зонам сбора граждан и деятельности. См. Нашу серию из 50 общественных центров, их планы и разделы ниже.
Centro Cultural y Ecológico Imagina / TIBÁrquitectos
© Адам Уайзман через TIBÁrquitectos через TIBÁrquitectos Культурный центр Арауко / elton_léniz
© Felipe Díaz Contardo via elton_lizniz через elton_lizné через elton_lizné .Быть домом культуры в движении / MVRDV + ADEPT © Адам Мёрк через MVRDV + ADEPT через MVRDV + ADEPT Бетон на проспекте Альсеркал / OMA
© Мохамед Сомджи, Cortesía Alserkal Avenue через OMA A через OMA A и культурный центр / Mecanoo + КОД: arkitektur Cortesía de Mecanoo через Mecanoo + CODE arkitektur Культурный центр фонда Ставроса Ниархоса / Строительная мастерская Ренцо Пьяно
Cortesía de SNFCC. через Renzo Piano Building Workshop через Renzo Piano Building Workshop Дом культуры / KÜHNLEIN Architektur
© Erich Spahn через KÜHNLEIN Architektur через KÜHNLEIN Architektur Центр искусств и культуры Форт-Мейсон / © LMS Architece 905 LMS Architects
через LMS Architects Centre Culturel de Notre-Dame-de-Grâce / AFO — Atelier Big City, FSA Architecture Inc и L’OEUF Architects в консорциуме
© Стив Монпетит через Atelier Big City через Atelier Big City Культурный центр и библиотека De Factorij / ebtca architecten & Archiles architecten
© Деннис Де Смет via ebtca architecten & Archiles architecten via ebtca architecten & Archiles architecten Maison De La Culture / Atelier 56S
© Jeretelmias 56S via Atelier 56S CorpArtes Theater and Cultural Center / Renzo Zecchetto Architects
© Guy W enborne через Renzo Zecchetto Architects через Renzo Zecchetto Architects Estación Cultural Tecpatán / Oficina de Diseño y Taller Brigada de Arquitectura
© Adrián Llaguno via Oficina de Biseño de Arquitectura
Plaza культуры Норте / Оскар Гонсалес Moix
© Рамиро дель Карпио через Оскар Гонсалес Moix через Оскар Гонсалес Moix Эль Tranque культурный центр / БиС Arquitectos
© Juan Francisco Vargas через БиС Arquitectos через БиС Arquitectos Centro де Арте y Cultura / FURMAN-HUIDOBRO arquitectos asociados
© Nico Saieh via FURMAN-HUIDOBRO arquitectos asociados Культурный центр и музыкальная школа / Alberich-Rodríguez Arquitectos asociados
Севилья / Васкес Консуэгра © Duccio Ma lagamba через Васкес Консуэгра через Васкес Консуэгра Культурный центр Cobquecura / Альберто Кампо Баеза
через Альберто Кампо Баеза через Альберто Кампо Баеза Культурный центр Пасси / Бекманн Н’Тепе 905 Beckmann N’Thepe
Культурный центр Габриэлы Мистраль / Cristián Fernández Arquitectos + Lateral Arquitectura & Diseño
© Nico Saieh via Cristián Fernández Arquitectos + Lateral arquitectura & Discovery 905 Arquitetura © Nelson Kon через Brasil Arquitetura через Brasil Arquitetura Nave 16 Matadero Madrid / ICA Arquitectura
Cortesía de Iñaqui Carnicero через ICA Arquitectura через ICA Arquitectura через ICA Arquitectura через ICA Arquitectura Forcent 905 через ICA Arquitectura Forcent 905 через ICA Arquitectura 905 через ICA Arquitectura 905 Архитекторы © FG + SG через EXIT Archit ects via EXIT Architects Centro Cultural Casal Balaguer / Flores & Prats + Duch-Pizá
Cortesía de Flores & Prats Arquitectos via Duch-Piza Arquitectos + Flores & Prats via Duch-Piza Arquitectos 905 Jota Prats 905 & Prats 905 & Flores Культурный центр / G /// bang © Энрик Дуч via G /// bang via G /// bang Культурный центр Виана-ду-Каштелу / Эдуарду Соуто де Моура
© Жоао Моргадо — Архитектурная фотография via Eduardo Souto де Моура через Эдуардо Соуто де Моура Культурный центр Седан / Richard + Schoeller Architectes
© Серджио Грация через Richard + Schoeller Architectes через Richard + Schoeller Architectes Японский культурный центр D.
Р. Конго / Университет Кейо SFC Лаборатория Хиронори Мацубара через Токио Мацубара и архитекторы через Университет Кейо Лаборатория Хиронори Мацубара Университета Кейо Цен через Университет Кейо Лаборатория Хиронори Мацубара Университет Кейо Центр Гейдара Алиева / Zaha Hadid Architects © de de la Corona. Hadid Architects Cortesía de Zaha Hadid Architects Культурный центр в Катовице / Рафал Мазур
© Джоанна Новицка через Рафаля Мазура Культурный центр Даоиз и Веларде / Рафаэль Де Ла-Хоз
© Альфонсо Де Ла-Хоз через Рафель Де Ла-Хоз © Альфонсо Де Ла-Хос 45 via Rafael De La-Hoz Niigata City Konan Ward Cultural Center / Chiaki Arai Urban and Architecture Design
© Taisuke Ogawa via Chiaki Arai Urban and Architecture Design via Chiaki Arai Urban and Architecture Design Культурный центр Les Quinconces / Babin + Рено
© Сесиль Септет © Бабин + Рено © Бабин + Рено Centro Cultur al Palacio La Moneda y Plaza de la Ciudadanía / Undurraga Devés Arquitectos
© Guy Wenborne via Undurraga Devés Arquitectos через Undurraga Devés Arquitectos Akiha Ward C Urban Center и Chiaki Arai 9029 © Ogawa Ward C Urban Center и Chiaki Arai 9029 © Ogawa Ward C Urban Center / Chiaki Arai 9029 © Урбанистический центр Чиакиис Араи 45 Архитектурный дизайн
через Чиаки Араи Городской и архитектурный дизайн Культурный центр пустыни Нк’Мип / DIALOG
© Nic Lehoux Photography via DIALOG Культурный центр и марражный зал Эйюп / Emre Arolat Architects
© Cemal Emden via Emre Arolat via Emre Arolat Architects Centro Cultural Caixa Forum Barcelona / Arata Isozaki
© Felipe Ugalde via Arata Isozaki via Arata Isozaki Музыкальный культурный центр / Eduardo de Miguel Arbonés
de Miguel Arbonés Культурный центр в Сен-Жермен-ле-Арп ajon / Ateliers OS Architectes
через Ateliers OS Architectes через Ateliers OS Architectes через Ateliers OS Architectes Культурный центр Служевского / WWAA + 307kilo
© Rafał Kłos через WWAA + 307 Kilo Design через WWAA + 307 Kilo Design через WWAA + 307 Kilo Design Культурный центр / Castañeda, Cohen, Nanzer, Saal, Salassa, Tissot © Gonzalo Viramonte via Castañeda, Cohen, Nanzer, Saal, Salassa, Tissot via Castañeda, Cohen, Nanzer, Saal, Salassa, Rad28945 Cultural Centre, Bad28945 / Gangoly & Kristiner Architects © Paul Ott via Gangoly & Kristiner Architects via Gangoly & Kristiner Architects Культурный центр La Gota — Музей табака / Losada García
© Miguel de Guzman via Losada García 45 via 905a García Культурный центр / Airaudo + Caballero + Giménez Rita + Llonch © Federico Cairoli via Airaudo + Caballero + Giménez Rita + Llonch via Airaudo + Caballero + Giménez Rita + Llonch Теплообменник Važecká / Atrium Architekti
© Lubo Stacho, через Architektonické štúdio Atrium через Architektonické štúdio Atrium через Architektonické štúdio Atrium ETAREA + PROAHEALI CELINEDO Atrium + Micarea Center + PROAIRA + PROAAAREA2 © Андреа Босио через AREA PROGETTI + UNA2 + Андреа Мишелини + Лаура Чеккарелли через AREA PROGETTI + UNA2 + Андреа Мишелини + Лаура Чеккарелли Культурный центр / Архитектура Auneau Архитектура Патрика Патрика 9045 через Мишель Патрик Денанс 9045 © Мишель Патрик Денанс 9045 через Мишель Патрик Денанс 9045 Mauger
Комплексные числа: умножение
Комплексные числа: умножение
Умножение производится алгебраически.
Сложное умножение — это более сложная операция для понимания с алгебраической или геометрической точки зрения. Давайте сначала сделаем это алгебраически, а для умножения возьмем определенные комплексные числа, например 3 + 2 i и 1 + 4 i. В каждом есть два члена, поэтому, когда мы их умножим, мы получим четыре члена: (3 + 2 i ) (1 + 4 i ) = 3 + 12 i + 2 i + 8 i ².
Теперь 12 i + 2 i упрощается до 14 i, конечно.А как насчет 8 i ²? Помните, что мы ввели i как сокращение для √ – 1, квадратного корня из –1. Другими словами, i — это то, что имеет квадрат –1. Таким образом, 8 i ² равно –8. Следовательно, произведение (3 + 2 i ) (1 + 4 i ) равно –5 + 14 i.
Если вы обобщите этот пример, вы получите общее правило умножения
Помните, что ( xu — yv ), действительная часть продукта, является произведением реальных частей минус произведение мнимых частей, но ( xv + yu ) мнимая часть продукт, представляет собой сумму двух произведений одной действительной части и другой мнимой части.
Давайте посмотрим на некоторые частные случаи умножения.
Умножение комплексного числа на действительное
В приведенной выше формуле умножения, если v равно нулю, вы получите формулу для умножения комплексного числа x + yi и действительного числа u вместе: ( x + yi ) u = xu + yu i .
Другими словами, вы просто умножаете обе части комплексного числа на действительное число.Например, 2 умножить на 3 + i будет просто 6 + 2 i. Геометрически, когда вы удваиваете комплексное число, просто удваиваете расстояние от начала координат, 0. Точно так же, когда вы умножаете комплексное число z на 1/2, результат будет на полпути между 0 и z. Умножение на 2 можно рассматривать как преобразование, которое растягивает комплексную плоскость C на коэффициент 2 от 0; и умножение на 1/2 как преобразование, которое сжимает C до 0.
Умножение и абсолютное значение.
Несмотря на то, что мы сделали только один случай для умножения, достаточно предположить, что абсолютное значение zw (то есть расстояние от 0 до zw ) может быть абсолютным значением z , умноженным на абсолютное значение . ш. Это было тогда, когда w было действительным числом u чуть выше. На самом деле это так в целом:
Проверка этого тождества — это упражнение по алгебре.Чтобы доказать это, мы докажем, что это верно для квадратов, поэтому нам не придется иметь дело с квадратными корнями. Мы покажем | zw | ² = | z | ² | w | ². Пусть z будет x + yi, и пусть w будет u + vi. Тогда, согласно формуле умножения, zw равно ( xu — yv ) + ( xv + yu ) i. Вспомните из раздела об абсолютных величинах, что
| z | ² = x ² + y ²
Аналогично имеем
| w | ² = u ² + v ²
и, поскольку zw = ( xu — yv ) + ( xv + yu ) i,
| wz | ² = ( xu — yv ) ² + ( xv + yu ) ²
Итак, чтобы показать | zw | ² = | z | ² | w | ², все, что вам нужно сделать, это показать, что
( xu — yv ) ² + ( xv + yu ) ² = ( x ² + y ²) ( u ² + v ²)
и это простое упражнение по алгебре.
Полномочия
i. В нашем следующем частном случае умножения рассмотрим различные степени мнимой единицы i. Мы начали с предположения, что i ² = –1. Что насчет i ³? Это просто i ² умножить на i , и это будет -1 умножить на i. Следовательно, i ³ = — i. Что интересно: куб i — это собственное отрицание.Далее рассмотрим i ⁴. Это квадрат i ², то есть квадрат –1. Итак, i ⁴ = 1. Другими словами, i — это корень четвертой степени из 1. Вы можете показать, что — i — это еще один корень четвертой степени из 1. И поскольку и –1, и 1 являются квадратными корнями из 1, теперь мы знаем все четыре корня четвертой степени из 1, а именно, 1, i, –1 и — i. Это наблюдение связано с фундаментальной теоремой алгебры, поскольку уравнение z ⁴ = 1 является уравнением четвертой степени, поэтому должно иметь ровно четыре корня.
Более высокие степени i легко найти теперь, когда мы знаем i ⁴ = 1. Например, i ⁵ равно i умножить на i ⁴, и это всего лишь i. . Можно уменьшить мощность i на 4 и не изменить результат. Другой пример: i ¹¹ = i ⁷ = i ³ = — i.
Как насчет отрицательных степеней и ? Что является обратным для i, то есть i ^–1? По той же причине, что вы можете вычесть 4 из степени i и не изменить результат, вы также можете прибавить 4 к степени i. Это означает i ^–1 = i ³ = — i. Таким образом, i обратное — i. Представьте себе — число, обратное значение которого — собственное отрицание! Конечно, легко проверить, что i раз — i равно 1, поэтому, конечно, i и — i являются обратными.
Корни единства.
Различные корни из 1 называются корнями из единицы. В общем, по Фундаментальной теореме алгебры количество n корней -й степени из единицы равно n, , так как существует n корней у уравнения n -й степени. z ^u — 1 = 0.Квадратные корни из единицы равны 1 и –1. Корни четвертой степени равны ± 1, ± i, , как отмечалось ранее в разделе, посвященном абсолютным значениям. Кроме того, в этом разделе упоминалось, что ± √2 / 2 ± i √2 / 2 были квадратными корнями из i и — i, и теперь с формулой умножения, которую легко проверить. Следовательно, восемь корней восьми из единицы равны ± 1, ± i, и ± √2 / 2 ± i √2 / 2. Обратите внимание на то, как эти восемь корней единицы равномерно распределены по единичной окружности.
Мы можем использовать геометрию, чтобы найти некоторые другие корни из единицы, в частности кубические корни и корни шестой степени из единицы. Но давайте их немного подождем.
Умножение комплексного числа на
i. В нашей цели по поиску геометрической интерпретации комплексного умножения, давайте рассмотрим следующее умножение произвольного комплексного числа z = x + yi на i. z i = ( x + yi ) i = — y + xi .
Давайте интерпретируем это утверждение геометрически. Точка z в C расположена на x единиц справа от мнимой оси и на y единиц выше действительной оси. Точка z i расположена на y единиц слева и x единиц выше. Произошло то, что умножение на i повернулось в точку z на 90 ° против часовой стрелки вокруг начала координат до точки z i. Короче говоря, умножение на i дает поворот на 90 ° против часовой стрелки на 0.
Вы можете проанализировать, что происходит при умножении на — i таким же образом. Вы обнаружите, что умножение на — i дает поворот на 90 ° по часовой стрелке примерно на 0. Когда мы не указываем против часовой стрелки или по часовой стрелке при обращении к поворотам или углам, мы будем следовать стандартному соглашению, которое подразумевается против часовой стрелки. Тогда мы можем сказать, что умножение на — i дает поворот на –90 ° вокруг 0 или, если хотите, поворот на 270 ° вокруг 0.
Геометрическая интерпретация умножения.
Чтобы полностью оправдать то, что мы собираемся увидеть, необходима тригонометрия, и это делается в необязательном разделе. А пока посмотрим на результаты без обоснования. Мы видели два особых случая умножения: один на действительные числа, что приводит к масштабированию, другой на и , что приводит к вращению. Общий случай — это комбинация масштабирования и вращения.
Пусть z и w будут точками на комплексной плоскости C .Проведите линии от 0 до z и от 0 до w . Длины этих строк — абсолютные значения | z | и | w | соответственно. Мы уже знаем, что длина строки от 0 до zw будет абсолютным значением | zw | что равно | z | | Вт |. (На диаграмме | z | составляет около 1,6, а | w | составляет около 2,1, поэтому | zw | должно быть около 3,4. Обратите внимание, что единичный круг заштрихован.) Чего мы не знаем, так это направления линии от 0 до zw.
Ответ: «углы складываются». Мы определим направление линии от 0 до z по определенному углу, называемому аргументом z , иногда обозначаемым arg ( z ). Это угол, вершина которого равна 0, первая сторона — положительная действительная ось, а вторая сторона — прямая от 0 до z. Другая точка w имеет угол arg ( w ).Тогда произведение zw будет иметь угол, который является суммой углов arg ( z ) + arg ( w ). (На диаграмме arg ( z ) составляет около 20 °, а arg ( w ) составляет около 45 °, поэтому arg ( zw ) должно быть около 65 °. )
Таким образом, у нас есть два уравнения, которые определяют, где находится zw в C :

Wolfram | Примеры альфа: комплексный анализ
Другие примеры
Комплексные числа
Анализировать свойства функций комплексной переменной или выполнять основную арифметику, находить корни или применять функции к комплексным числам.
Выполните основную арифметику над комплексными числами:
Примените функции к комплексным числам:
Другие примеры
Комплексные функции
Построить график функций комплексной переменной или вычислить и проанализировать их свойства.
Вычислить свойства функции сложной переменной (используйте переменную z ):
Другие примеры
Поляки
Обнаружение полюсов сложной функции в указанной области или на всей комплексной плоскости.
Найдите полюса сложной функции:
Найдите полюса в указанном домене:
Другие примеры
Остатки
Вычислить остатки функций на комплексной плоскости в точке или в указанной области.
Вычислить остаток функции в точке:
Вычислить вычеты в полюсах функции:
Вычислить остатки на полюсах в указанном домене:
Другие примеры
Римановы поверхности
Вычисление и визуализация римановых поверхностей для сложных функций.
Визуализируйте риманову поверхность:
Другие примеры
Комплексные числа
Представление комплексных чисел
Все комплексные числа z = a + bi представляют собой «комплекс» всего из двух частей:
Действительная часть : Re (z) = a
Мнимая часть : Im (z) = b
Когда Re (z) = 0, мы говорим, что z равно чисто мнимому ; когда Im (z) = 0, мы говорим, что z — это чисто вещественное .
Re (z) и Im (z) являются действительными числами. Таким образом, любое комплексное число можно представить как упорядоченную пару действительных чисел (a, b). Мы знаем все об упорядоченных парах действительных чисел. Чтобы визуализировать их, мы наносим их на плоскость:
Это изображение комплексной плоскости (часто называемое диаграммой Аргана, хотя идея обычно приписывается Весселю) позволяет нам назначать некоторые знакомые атрибуты комплексным числам.
Например, мы назначаем «размер» действительным числам x, задав абсолютное значение | x | .Это говорит нам, как далеко x от начала координат, независимо от его направления. Точно так же мы можем измерить расстояние r комплексного числа z от начала координат, используя формулу декартового расстояния:
Этот «размер» комплексного числа часто называют его модулем .
Точно так же каждому действительному числу назначено «направление»: либо +, либо -, в зависимости от того, идем ли мы вправо или влево от начала координат соответственно. На картинке выше видно, что для сложных чисел не все так просто.Комплексные числа могут отходить от начала координат в любом направлении циферблата. Чтобы указать направление, мы даем угол q, измеренный против часовой стрелки вверх от оси x до отрезка линии, содержащего начало координат и комплексное число. Обратите внимание, что:
Это «направление» комплексного числа часто называют его аргументом .
Разница между описанием комплексного числа с помощью пары (a, b) и пары (r, q) заключается в разнице между использованием декартовых координат и полярных координат соответственно.
Просмотр полярных координат
В следующем примере показано, как полярные координаты (r, q), подобные тем, которые используются для описания комплексных чисел, также могут использоваться для упрощенного описания кривых с определенной «полярной» симметрией:
Изучите полярные кривые
Две приведенные выше формулы для модуля r и аргумента q в терминах a и b обеспечивают своего рода «перевод» между двумя системами представления.
Страница не найдена | Ларсон Precalculus — Precalculus 9e
MathArticles.com предоставляет соответствующие статьи из известных математических журналов. Статьи согласованы по тематике исчисления Ларсона. Посетите MathArticles.com, чтобы получить доступ к статьям из:
Журнал
Организации
AMATYC Обзор
Американская математическая ассоциация двухгодичных колледжей
Американский математический ежемесячник
Математическая ассоциация Америки
Журнал математики колледжа
Математическая ассоциация Америки
Журнал химического образования
Американское химическое общество
Математические горизонты
Математическая ассоциация Америки
Математический вестник
Математическая ассоциация (Великобритания)
Математический журнал
Математическая ассоциация Америки
Учитель математики
Национальный совет учителей математики
Учитель физики
Американская ассоциация учителей физики
Scientific American
Scientific American
Журнал UMAP
Консорциум математики и ее приложений
.
No related posts.

Давайте снова воспользуемся 3 + 4i :

Вот в полярной форме:

Журнал	Организации
AMATYC Обзор	Американская математическая ассоциация двухгодичных колледжей
Американский математический ежемесячник	Математическая ассоциация Америки
Журнал математики колледжа	Математическая ассоциация Америки
Журнал химического образования	Американское химическое общество
Математические горизонты	Математическая ассоциация Америки
Математический вестник	Математическая ассоциация (Великобритания)
Математический журнал	Математическая ассоциация Америки
Учитель математики	Национальный совет учителей математики
Учитель физики	Американская ассоциация учителей физики
Scientific American	Scientific American
Журнал UMAP	Консорциум математики и ее приложений