- Математика (алгебра, геометрия)
- Начальная школа
- Кафедра физико-математического образования
- Главная | My test site
- МБОУ Школа №116 г.о. Самара
- «Всероссийские проверочные работы 2021–2022 в школе и СПО»
- Педагогический состав
- (PDF) Изучение методологии решения математических задач в начальном образовании
- (PDF) Методология исследования и образование по критической математике
- Количественная методология анализа влияния формулировки математического задания на оценку успеваемости учащихся
- Методология математики tok
- Устранение гендерного разрыва в математике с помощью методик активного обучения | IZA
- Обзор: Методология преподавания математики
- 14 стратегий преподавания математики
- 1. Поднимите планку для всех
- 2. Не ждите — действуйте прямо сейчас!
- 3.
- 4. Наблюдать, изменять и переоценивать
- 5. Подключите математику к другим областям обучения
- 6. Персонализируйте и предложите выбор
- 9. Делайте упор на практическом обучении
- 10. Стремитесь к пониманию
- 11. Выбирайте значимые задачи.
- 12. Разрешить продуктивную борьбу
- 13. Создавайте азарт и поощряйте прогресс
- 14. Поощряйте совместную работу учителей и размышления
Математика (алгебра, геометрия)
27.10.2021 г
Всероссийская олимпиада школьников по математике в 2021-2022 учебном году.
Школьный тур проходит на платформе СИРИУС. На этом сайте вы можете ознакомиться с текстами заданий, которые предлагались детям во время школьного тура, и посмотреть вместе со школьниками видеоразборы решений.
ССЫЛКА НА САЙТ ШКОЛЬНОГО ТУРА
Предварительные результаты школьников доступны на платформе СИРИУС по персональному коду участника.
ССЫЛКА НА ПЛАТФОРМУ
Имея список участников и коды, образовательная организация имеет возможность составить список реальных участников школьного тура и начать готовить отчёт. Зелёные столбцы НЕ заполняйте!
ССЫЛКА НА ФОРМУ ОТЧЁТА
Районный тур олимпиады состоится 4 декабря.
Информация по организации районного тура будет опубликована позднее.
Внимание!
Уважаемые коллеги!

Обратите внимание обучающихся, что в связи с редакторской ошибкой задача 7 в 4 классе засчитана всем участникам на максимальный балл. Задача 2 в 4 классе допускала двойную трактовку. Ответы были засчитаны по любой из этих трактовок.
С уважением, Естественнонаучный сектор Центра Олимпиад СПб.
27.09.2021 г
Уважаемые педагоги, кадровый мониторинг нужно пройти до 04.10.2021 г
ССЫЛКА
Уважаемые коллеги!
Пожалуйста, доведите информацию до учителей.
В период с 26 мая по 6 июня 2021 года кафедра математического образования и информатики СПб АППО проводит краткосрочные курсы повышения квалификации по программе Развитие и оценивание функциональной грамотности обучающихся (по направлению «Математическая грамотность») в контексте международных исследований качества образования» в объеме 36 часов на хозрасчетной основе.
Занятия проводятся в очно-заочном формате с 15.00.
Контактный телефон центра платных услуг и маркетинга 409-82-83.
Можно звонить на кафедру 409-82-84.
19.02.2021
Уважаемые педагоги, приглашаем вас к участию в районном конкурсе «Мастерская педагогического опыта: от идеи до воплощения».
ПОЛОЖЕНИЕ о конкурсе
РЕГИСТРАЦИЯ
18.12.2020
Уважаемые педагоги, обучающиеся и родители.
Информация об итогах районного этапа должна была поступить из Центра олимпиад до 25 декабря 2020 г.
Сегодня 18 декабря вы можете ознакомиться с результатами
6 класса 7 класса 8 класса 9 класса 10 класса 11 класса
Информации об участниках, приглашённых на региональный этап ещё не посупило.
Список победителей и призёров районного этапа олимпиады в Невском районе смотрите здесь.
03.11.2020
Уважаемые коллеги, изменились требования к подаче документов на аттестацию. Вся информация по аттестации представлена ниже в Направлении «Новые возможности для каждого».
Ссылка для открытия в новом окне
*
Уважаемые председатели ШкМО учителей математики, убедительно просим вас до 24.10.2020 на наш электронный адрес прислать письмо с вашей действующей рабочей почты. В теме письма напишите МО, в тексте ваши ФИО и рабочий телефон для связи. Извините, но очень много сбоев в отправке вам писем и в координировании нашей с вами работе. Благодарим за сотрудничество.
*
до 24.10.2020 (если Вы не отправляли сведения в ранее в этом учебном году

Ссылка
*
28-31 сентября 2020 года состоялся школьный этап ВсОШ по математике в 2020-2021 уч.году.
Задания
Критерии
Форма для отчёта по проведению школьного тура.
*
24.09.2020
Уважаемые коллеги, 24 сентября совещание председателей ШкМО будет проводиться на платформе Zoom.
Тема: Организация учебно-методической работы в 2020-2021 учебном году
Время: 24 сен 2020 15:30.
Подключиться к конференции Zoom
https://us04web.zoom.us/j/74079986874?pwd=WlBudGlCaUhmU1owRk0yVTRPMjZwUT09
Идентификатор конференции: 740 7998 6874
Код доступа: W5VswQ
Лист регистрации
*
09.09.2020
Уважаемые коллеги, 10 сентября мы проведём первую встречу в 2020-2021 учебном году. Встреча будет проходить дистанционно с помощью приложения ZOOM.
Встреча будет проходить дистанционно с помощью приложения ZOOM.
Начало: 16.00
Продолжительность: 30 минут
Речь пойдёт о формах взаимодействия педагогов и предстоящих ВПР.
ССЫЛКА
Уважаемые коллеги, все методические материалы и подсказки смотрите на этой странице в разделе «Современная школа».
Уважаемые коллеги!
С 06 апреля 2020 года в соответствии с Распоряжением Комитета по образованию Санкт-Петербурга от 24.03.2020 №818-р «Об организации деятельности образовательных организаций Санкт-Петербурга» обучение будет осуществляться с применением электронного обучения и дистанционных образовательных технологий.
С последними Нормативными документами можно ознакомиться на сайте ИМЦ в разделе Новости.

http://imc-nev.ru/imts/distantsionnoe-obuchenie.html
Раздел сайта ИМЦ, посвященный использованию ДОТ (дистанционным образовательным технологиям), будет постоянно обновляться. Уже сейчас в разделе можно ознакомиться с методическими материалами, рекомендованными электронными ресурсами, перечнем уроков образовательных платформ и портала ДО по предметам и классам и другими актуальными материалами.
Методические рекомендации Минпросвещения России по реализации образовательных программ начального общего, основного общего, среднего общего образования, образовательных программ среднего профессионального образования и дополнительных общеобразовательных программ с применением электронного обучения и дистанционных образовательных технологий
Ознакомление с оперативной информацией:
(c 06.04.2020г.)
* 20 февраля 2020 года в 5-х и 7-х классах были проведены региональные диагностические работы по функциональной грамотности.
Информацию о работах читать здесь.
Подробнее о функциональной грамотности можно читать здесь (матем.грам.), здесь (финансов.грам.) и здесь (читат.грам.).
Тексты работ: Варианты 5-1 5-2 7-1 7-2
* Материалы семинара по решению задач с параметрами 28.10.2019 г
Презентация Задачи
* Материалы семинара по новому формату ОГЭ от Циовкина
Скачать ч1 Скачать ч2 Скачать ч3
Начальная школа
Методика решения текстовых задач
Введение
Решение текстовых задач, как хорошо известно, является наиболее действенным способом научиться понимать и полюбить математику. Их надо решать систематически на протяжении 1−11 классов, а также текстовые задачи по физике и геометрии, химии. Для цели овладения математикой созданы современные высококачественные пособия [1−3]. Кроме того не устарели и гениальные творения Дж.Пояй “Как решить задачу” и “Математическое открытие”, а также хорошо продуманные текстовые задачи, которые приведены (гл.
Данное пособие (части I − VI) предназначено главным образом для учеников начальных 1 −4 классов, но также для их родителей и учителей (части VII−VIII).
В пособии по текстовым задачам для начальных классов [1] представлены задачи на все основные темы школьной программы, изучаемых в начальной школе. Однако методы решения задач в [1] не представлены. Данное пособие непосредственно связано с этим пособием и в скобках указаны номера задач по [1]. Рассматривается подробно
В части I рассмотрены примеры решения с помощью основного метода – по действиям, на все темы, которые представлены в [1]. Основной метод базируется на 4 действиях арифметики: сложения, вычитания, умножения, деления.
В части II рассмотрена подробно природа основного метода (по действиям), с помощью которого решаются все текстовые задачи начальной (и средней) школы (1 – 6 классы). Несмотря на то, что тематика, содержание и трудность задач самые разные, основой метод по действиям основывается всего на одно главномм логическом действие: Если…, то… . и вспомогательном логическом умножении. Именно на главном логическом действии основана вся математика. До сих пор ни в одном учебнике или пособии не отражается, явным способом, эта логическая суть математических методов.
Несмотря на то, что тематика, содержание и трудность задач самые разные, основой метод по действиям основывается всего на одно главномм логическом действие: Если…, то… . и вспомогательном логическом умножении. Именно на главном логическом действии основана вся математика. До сих пор ни в одном учебнике или пособии не отражается, явным способом, эта логическая суть математических методов.
В части III рассмотрен дополнительный к основному методу, метод геометрической иллюстрации количественных отношений в текстовой задаче, с помощью отрезков. Такая геометрическая иллюстрация особенно будет полезна в средней школе при изучении дробей, процентов.
В части IV рассматривается метод решения текстовых задач с помощью составления простейших уравнений. Большинство задач, которые решаются с помощью основного метода по действиям, могут быть решены и с помощью уравнений. Он дополняет и расширяет основной метод.
Он дополняет и расширяет основной метод.
В части V представлены задачи с буквами. Задачи с буквами по математической сути ничем не отличаются от задач с числами и решаются теми же методами, по действиям или с помощью уравнений, но они более абстрактны и вызывают у школьников подчас немалые трудности.
В части VI возможности применения простейших таблиц и графиков.
В части VII рассмотрены различные схемы решения текстовых задач по действиям. Хотя в основе метода по действиям лежит всего одно главное логическое действие: Если …., то…, тем не менее, последовательность его применения к исходным условиям задачи является иррациональным моментом при решении задач. Этот материал, видимо, можно рекомендовать учителю начальных классов, тогда как ученикам, можно рекомендовать знакомиться в более старших классах.
В части VIII даны основные понятия и правила действий, изучаемые в начальной школы, на знании которых только возможно осмысленное понимание методов решения задач. Лучше всего, по настоящий день, подробно и последовательно, эти сведения изложены в известном гениальном классическом учебнике прошлого [5].
Лучше всего, по настоящий день, подробно и последовательно, эти сведения изложены в известном гениальном классическом учебнике прошлого [5].
Литература
1. Узорова О.В., Нефёдова Е.А. 2500 задач по математике. 1-4 классы. М.: Астрель. 2011. (Аст. 2016, Аст. 2019)
2. Шевкин А.В. Текстовые задачи по математике. 5-6 классы.М.Илекса. 2015.
3. Шевкин А.В. Текстовые задачи по математике. 7-11 классы. М.Илекса. 2016.
4. Сбоник задач для поступающих во ВТУЗы/под ред. Сканави. М.И. М. Аст. 2015.
5. Шевченко Н.И. Арифметика. Учебник для 5 и 6 классов восьмилетней школы. Просвещение. 1965.
Кафедра физико-математического образования
Кафедра физико-математического образования является одним из подразделений Самарского областного института повышения квалификации и переподготовки работников образования, действующим, практически, с основания института.
Сотрудники кафедры: Гилев Александр Александрович – доцент, кандидат физико-математических наук; Петрукович Галина Георгиевна – преподаватель; Афанасьева Светлана Геннадьевна – кандидат педагогических наук, доцент; Логачёв Александр Андреевич – методист.
Математика и физика входят в состав цикла естественнонаучных дисциплин и по своему со¬держанию представляют собой повседневный рабочий инструмент специалиста в большинстве об¬ластей профессиональной деятельности. Без современной математики с ее развитым логическим и вычислительным аппаратом был бы невозможен прогресс в большинстве областей человеческой деятельности. Математика является не только мощным средством решения прикладных задач и универсальным языком науки, но и элементом общей культуры. Знания по физике формируют научное представление об окружающем мире, о его познаваемости человеком, о невозможности нарушений законов природы. Поэтому интерес и внимание к этим дисциплинам не ослабевает, а вопросы преподавания этих предметов не теряют своей актуальности.
Основными направлениями работы кафедры являются:
1. Проектирование и использование многоуровневой системы задач в процессе обучения математике и физике в средней школе.
2. Дифференцированное обучение математике и физике в основной школе.
3. Дифференцированное обучение математике и физике в старшей школе.
4. Преемственность в обучении математике и физике между начальной, основной и старшей школой.
5. Предпрофильная подготовка учащихся основной школы в процессе изучения математики и физики.
6. Профильное обучение учащихся в процессе изучения математики и физики в средней (полной) школе.
7. Организация и содержание подготовки учащихся к математическим и физическим олимпиадам.
8. Организация учебно-исследовательской и проектной деятельности учащихся. Консультирование учащихся при подготовке докладов к научным конференциям.
9. Содержание и руководство методической работой учителей математики и физики.
10. Разработка учебно-методических пособий для подготовки учащихся к ЕГЭ и ОГЭ.
11. Информирование и ознакомление педагогических работников с изменениями в учебных программах и новыми учебно-методическими комплектами по математике и физике.
12. Ознакомление учителей математики и физики с инновационными технологиями обучения.
13. Консультации для работников образования по вопросам модернизации математического и физического образования и аттестации учащихся основной и средней школ.
14. Консультации для учителей математики и физики по вопросам их аттестации, участию в конкурсах профессионального мастерства.
Все направления работы, связанные с математикой, нацелены на реализацию Концепции математического образования в Российской федерации.
На кафедре ежегодно издаются монографии, учебно-методические пособия, учебные пособия, сборники материалов научных конференций. Преподаватели кафедры принимают активное участие в Международных и региональных научных конференциях.
Основные публикации А.А.Гилева, к.ф.-м.н., доцента доступны по ссылкам:
1. Научные и методические публикации
2. Программы повышения квалификации
3. Физика Средняя школа Уроки
Контактная информация. Телефон: 8(846)242-65-70. E-mail: [email protected].
Концепция развития математического образования в Российской Федерации
Материалы выступающих на конференции по ФГОС 2015, секция 13 Материалы выступающих на конференции по ФГОС 2015, секция 13.
 1 Материалы выступающих на конференции по ФГОС 2015, секция 13.2 Материалы выступающих на конференции по ФГОС 2015, секция 18
1 Материалы выступающих на конференции по ФГОС 2015, секция 13.2 Материалы выступающих на конференции по ФГОС 2015, секция 18Материалы выступающих на конференции по ФГОС 2015, секция 15
Опыт учителей Самарской области по работе с одарёнными детьми.Тренировочные материалы для подготовки к ЕГЭ по математике.
Тренировочные материалы для подготовки к ЕГЭ по биологии
Тренировочные материалы для подготовки к ОГЭ по биологии
Тренировочные материалы для подготовки к ОГЭ по биологии (продолжение)Тренировочные материалы для подготовки к ЕГЭ по биологии (продолжение)Тренировочные материалы для подготовки к ГИА по математике.
Материалы выступающих на региональной научно-практической конференции по ФГОС (секция №13) 18 сентября 2014 года
Материалы выступающих на Круглом столе с участием издательства «Просвещение» 7 октября 2014 годаСотрудники:
Кузнецов Владимир Петрович –доцент, кандидат физико-математических наук. |
Петрукович Галина Георгиевна —Преподаватель кафедры физико-математического образования СИПКРО |
Афанасьева Светлана Геннадьевна —доцент кафедры физико-математического образования, кандидат педагогических наук. |
Логачёв Александр Андреевич —методист |
Программы повышения квалификации
Главная | My test site
Консультации методистов →В ИМЦ создана форма, которую заполняют педагоги, обратившиеся к методисту (в любом формате по любому вопросу).
Прошу вас заполнять ее (будет проводиться мониторинг консультаций и анализ ваших обращений к методисту)!
Заранее благодарю!
28.10.2021
ФГБНУ «Институт стратегии развития образования Российской академии образования» проводит анкетирование учителей математики по вопросам формирования и оценки функциональной математической грамотности обучающихся.
Просим учителей математики пройти анкетирование (анонимное) →27.10.2021
1) Коллеги, сегодня появились предварительные результаты школьного тура Всероссийской олимпиады по математике.
Обратите внимание учащихся: в связи с редакторской ошибкой задача №7 в 4 классе засчитана всем участникам по максимальному баллу. Задача №2 в 4 классе допускала двойную трактовку. Ответы были засчитаны по любому из двух вариантов трактовок.
Задача №2 в 4 классе допускала двойную трактовку. Ответы были засчитаны по любому из двух вариантов трактовок.
После публикации официальных результатов прошу отчеты №1 и №2 отправлять по эл.почте на адрес [email protected] (с указанием номера ОО вместо трех нулей в названии файлов).
2) Форма отчета №2 исправлена! →26.20.2021
1) Создается группа для переобучения экспертов ОГЭ из других регионов.
Прошу председателе МО до 10 ноября сообщить (по тел. или эл.почте) о тех учителях, которые были экспертами ОГЭ в других регионах и еще не принимали участие в проверке работ школьников Санкт-Петербурга.
2) 10-12 ноября состоится РДР по математике в 6 классах (список ОО, принимающих участие в написании работы утвержден КО).
Материалы (приказы, распоряжения, КИМ, инструкции, отчеты) →Спецификация (см. п.6 План работы) →3) Документы для организации игры «Смарт Кенгуру» →25.10.2021
1) Информация совещания → 2) Про олимпиады → 3) Положение о конкурсе «Петербургский урок» → 4) Сайт ЦНППМ → Информация для учителей по работе с конструктором индивидуальной траектории профессионального роста →Прошу председателей МО и по желанию других коллег зарегистрироваться на сайте и пройти тестирование.
Благодарю!
5) План на ноябрь →
!!!25 октября 2021 года состоится совещание для председателей МО учителей математики!!!
Место проведения: ГБУ ИМЦ Выборгского района (Ярославский пр., д.72)
Начало в 11.00.
При себе необходимо иметь СИЗ (маски).
14.10.2021
14 октября состоится вебинар по «ЕГЭ по математике 2021: анализ результатов».
Ведущий: Ренев Олег Вадимович, заместитель председателя региональной предметной комиссии ЕГЭ по математике, учитель математики Губернатрского ФМЛ №30.
Предварительная регистрация →Ссылка на подключение в Teams →13.10.2021
1) Спецификация региональной диагностической работы для 6 классов, которая состоится 10-12 ноября →2) 19 октября в лекционном зале АППО состоится семинар А.Г.Мордковича. Начало в 15.30.
3) 25 ноября на базе ИМЦ Красносельского района состоится городской семинар «Функциональная грамотность (по направлению математическая грамотность): формирование и оценка». Начало в 16.00.
Начало в 16.00.
Приглашаются, в том числе, педагоги, имеющие опыт формирования ФГ и готовые поделиться успешными практиками.
Эл.почта Виноградовой Антонины Петровны (методиста Красносельского района): [email protected].
В письме необходимо указать ФИО, должность, ОУ и тему выступления.
05.10.2021
«Твой учитель не тот, кто тебя учит,
а тот, у кого учишься ты» Р. Бах
У нас есть чему поучиться! →Мы умны! Мы прекрасны! Мы любим! Мы любимы!
У нас получается всё хорошо и отлично!
Будем здоровы и счастливы!
27.09.2021
17 октября для учащихся 5-7 классов состоится математический Кубок «Раз-два-три«.
Время: с 12.00 до 14.00.
Формат: дистанционный.
Подробная информация →22.09.2021
Коллеги, спасибо за оперативность. Группа на курсы РЦОКОиИТ набрана!
21. 09.2021
09.2021
В ноябре стартуют краткосрочные курсы повышения квалификации «Особенности подготовки выпускников образовательных организаций к ГИА 9 (математика)». По окончании выдается удостоверение РЦОКОиИТ,
Квота для нашего района — 3 человека.
Расписание занятий →Желающих и имеющих возможность пройти эти курсы прошу определиться и сообщить о своем намерении по эл.почте ([email protected]) или телефону (8-911-011-61-81). Срок — до 27 сентября.
15.09.2021
1) Материалы для подготовки к школьному этапу Всероссийской олимпиады школьников по математике, проводимой с использованием информационного ресурса «Онлайн-курсы» образовательного центра «Сириус» →2) Информация о проведении открытой городской олимпиады «Математика НОН-СТОП» → 3) Информация о проведении Санкт-Петербургской открытой математической олимпиады для обучающихся начальной школы →
09.09.2021
11 сентября 2021 года (суббота) в ФМЛ №30 состоится ежегодная открытая олимпиада по математике для учащихся 5 классов.
13.08.2021
Уважаемые коллеги, в начале нового учебного года будут записываться видеоуроки для портала дистанционного образования Санкт-Петербурга.
В третьей четверти минувшего учебного года мы достойно справились с поставленной КО задачей!
Теперь нашему району предстоит записать уроки лишь одной учебной недели, но всех параллелей.
Какая именно неделя достанется нашему району, пока не известно…
Примеры уроков можно посмотреть здесь.Это могут быть видеоуроки или озвученные презентации.
Прошу тех, кто сможет принять участие в записи уроков, сообщить по электронной почте ([email protected]).
Возможно, вдвоем записывать уроки, например, для 5 класса.
ЮКЛАСОВА Людмила Алексеевна Заместитель директора по учебно-воспитательной работе |
||
НОВИКОВ Дмитрий Михайлович Заместитель директора по учебно-воспитательной работе |
||
ИВЧЕНКО Ольга Петровна Заместитель директора по воспитательной работе |
||
ЧУДАКОВ Сергей Николаевич Заместитель директора по административно-хозяйственной работе |
||
ШЕВЛЯКОВА Светлана Юрьевна Главный бухгалтер |
||
ФЕОКТИСТОВА Тамара Владимировна Учитель русского языка высшей категории |
||
НИКУЛЬШИНА Эльвира Эдуардовна Учитель русского языка |
||
ГЕЙДА Алёна Александровна Учитель русского языка первой категории |
||
КОСТИНА Светлана Владимировна Учитель русского языка |
||
ФИЛИМОНОВА Виктория Вячеславовна Учитель английского языка |
||
ПЕСТОВА Ольга Сергеевна Учитель английского языка |
||
ВАУЛИНА Екатерина Андреевна Учитель английского языка |
||
НИКУЛИНА Ирина Владимировна Учитель математики |
||
БАБУШКИНА Марина Вениаминовна Учитель математики |
||
ЮДИНА Ирина Викторовна Учитель математики высшей категории |
||
СОРОКИНА Наталья Вячеславовна Учитель математики и информатики первой категории |
||
ДАВЫДКИНА Галина Павловна Учитель физики |
||
КАЗАНЦЕВА Татьяна Николаевна Учитель химии и биологии |
||
БРЕНДОЕВА Виктория Сергеевна Учитель биологии |
||
МИНАЕВА Ксения Викторовна Учитель истории и географии |
||
ДЬЯЧЕНКО Людмила Валерьевна Учитель истории высшей категории |
||
УВАРОВА Кристина Александровна Учитель истории |
||
ДЕМЬЯНОВА Валентина Федоровна Учитель истории |
||
ГОНЧАР Нина Ивановна Учитель начальных классов |
||
ВОРОБЬЕВА Оксана Васильевна Учитель начальных классов |
||
МАСЛОВА Ольга Борисовна Учитель начальных классов |
||
ЛИСИНЦЕВА Яна Дмитриевна Учитель начальных классов |
||
МИНАЕВА Оксана Александровна Учитель начальных классов |
||
ФЕДОТКИНА Анастасия Вячеславовна Учитель начальных классов |
||
МУРЗИНА Елена Евгеньевна Учитель изобразительного искусства |
||
ЗЯБЛОВА Людмила Ивановна Учитель физической культуры |
||
ДОЛНИКОВА Анастасия Владимировна Учитель физической культуры | —>
||
ДУРЫГИНА Алла Владимировна Учитель технологии и ОБЖ |
||
СТЕПАНОВА Мария Андреевна Учитель музыки |
||
МАРЕЕВА Ксения Сергеевна Педагог-психолог |
||
БОРДАЧЕВА Татьяна Александровна Воспитатель ГПД |
«Всероссийские проверочные работы 2021–2022 в школе и СПО»
Дата и время проведения: 28 октября 2021 года в 18:00 (мск)
28 октября в 18:00 (МСК) приглашаем школьных учителей, преподавателей СПО на вебинар «Всероссийские проверочные работы 2021–2022 в школе и СПО».
В 2021 году ВПР впервые прошли в организациях среднего профессионального образования. Преподаватели колледжей и техникумов смогли не только подготовить студентов с использованием контента «ЯКласс», но и потренировать обучающихся на тестах ВПР для СПО 2021 на нашем сайте.
Как спланировать и регулярно вести подготовку к ВПР 2022 года по русскому языку, математике, истории, биологии, расскажут опытные педагоги и методисты нашей команды. Обновлённый функционал сайта позволяет усилить элементы цифровой дидактики в рабочей программе учителя. Мониторинг результатов самоподготовки, выдача проверочных тестов и работа над ошибками обучающихся стали ещё проще и удобнее для рядового учителя массовой школы.
На вебинаре мы подскажем приёмы работы на сайте для методических объединений школы или колледжа, расскажем, какие новые материалы в разделе ВПР на «ЯКласс» появятся в ближайшие месяцы.
Спикеры:
- методисты МЦ Виктория Галкина и Олеся Гончарова,
- редактор «ЯКласс» по физике Оксана Крысанова.

Проведёт вебинар руководитель Методического центра «ЯКласс» Марина Володина.
Участие в конференции бесплатное.
Все слушатели, которые зарегистрируются на конференцию на нашем сайте и подключатся к трансляции по ссылке из электронного письма, получат именные сертификаты (участники без подписки Я+) или именные свидетельства (участники с подпиской Я+).
| Ф.И.О | Должность | Степень, звание, категория | |
| 1. | Брюханова Ирина Анатольевна | учитель ИЗО и черчения | соответствие занимаемой должности |
| 2. | Бакум Наталья Анатольевна | методист | соответствие занимаемой должности |
| 3. | Гонштеин Денис Петрович | учитель физкультуры | соответствие занимаемой должности |
4. | Данченко Евгения Владимировна | учитель географии | соответствие занимаемой должности |
| 5. | Демидас Алёна Викторовна | педагог-психолог | соответствие занимаемой должности |
| 6. | Демьяненко Александр Евгеньевич | педагог проектной деятельности | соответствие занимаемой должности |
| 7. | Двоерядкина Наталья Николаевна | учитель математики | доцент, к.пед.н. |
| 8. | Дубинина Людмила Геннадьевна | учитель математики | учитель I категории |
| 9. | Дябкин Игорь Анатольевич | учитель русского языка, литературы и МХК | доцент, к.философ.н. |
| 10. | Ерёмина Виктория Владимировна | учитель математики | доцент, к.физ-мат.н. |
11. | Жмуркова Карина Евгениевна | учитель истории и обществознания | соответствие занимаемой должности |
| 12. | Закирова Юлия Анатольевна | учитель физики | соответствие занимаемой должности |
| 13. | Замятина Алена Викторовна | учитель английского языка | соответствие занимаемой должности |
| 14. | Иванашко Юлия Петровна | учитель английского языка | соответствие занимаемой должности |
| 15. | Козюра Виктория Евгеньевна | учитель математики | соответствие занимаемой должности |
| 16. | Кокамбо Юлия Дмитриевна | учитель обществознания | соответствие занимаемой должности |
| 17. | Лапин Андрей Валерьевич | учитель истории | соответствие занимаемой должности |
18. | Левченко Анна Александровна | учитель русского языка и литературы | соответствие занимаемой должности |
| 19. | Лескова Светлана Анатольевна | учитель биологии | доцент, к.хим.н. |
| 20. | Лясковская Яна Викторовна | учитель китайского языка | соответствие занимаемой должности |
| 21. | Мишаченко Константин Геннадьевич | учитель информатики | соответствие занимаемой должности |
| 22. | Мусиенко Алексей Валентинович | учитель истории и обществознания | соответствие занимаемой должности |
| 23. | Назаренко Валерия Романовна | учитель русского языка и литературы | соответствие занимаемой должности |
| 24. | Назаренко Наталья Викторовна | учитель информатики | соответствие занимаемой должности |
25. | Охотникова Галина Генриховна | учитель химии | доцент, к.хим.н. |
| 26. | Павельчук Анна Владимировна | учитель математики и информатики | к.физ-мат.н. |
| 27. | Полица Юлия Михайлова | учитель музыки | соответствие занимаемой должности |
| 28. | Рычкова Евгения Сергеевна | учитель экономики | доцент, к.экон.н. |
| 29. | Сарина Галина Васильевна | учитель китайского языка | соответствие занимаемой должности |
| 30. | Темников Валентин Сергеевич | учитель физики и естествознания | соответствие занимаемой должности |
| 31. | Пашегорова Анна Вячеславовна | педагог-организатор | соответствие занимаемой должности |
32. | Трубникова Алёна Владимировна | учитель иностранных языков | соответствие занимаемой должности |
| 33. | Шумилин Илья Викторович | учитель плавания | соответствие занимаемой должности |
| 34. | Яцевич Любовь Павловна | учитель немецкого языка | доцент, к.пед.н. |
(PDF) Изучение методологии решения математических задач в начальном образовании
Международный научно-исследовательский журнал (IJSR)
ISSN (Online): 2319-7064
Impact Factor (2012): 3.358
Volume 3 Issue 9 , Сентябрь 2014 г.
www.ijsr.net
Лицензия под лицензией Creative Commons Attribution CC BY
1. Изучение методов научного обучения,
2. Развитие способностей к индуктивным и дедуктивным рассуждениям,
3.
развитие способностей к элементарному моделированию и использование существующих или создание новых моделей для изучения
свойств объектов,
4. развитие навыков классификации изученных объектов,
развитие навыков классификации изученных объектов,
систематизация знаний, обнаружение причины —
следствие и структурированные отношения между
объектами на уровне уже достигнутых знаний.
5. Развитие навыков выбора инструментов и методов для достижения поставленной цели
, в соответствии с существующими условиями,
6.развитие навыков для обнаружения связи между
усвоенного материала с практической работой в жизни и
7. обучение основным качествам, характерным для научного
мышления.
К специальным развивающим функциям задач относятся:
1. формирование и развитие знаний и навыков до
дедуктивное подтверждение и отрицание математических утверждений,
2. развитие навыков планирования решения данной задачи, до
исключить неважную информацию из проблемы и добавить к
недостающую информацию, чтобы выбрать методы, инструменты
и операции для решения проблемы, а также проверить точность
и смысл решения,
3. формирование четкого представления о логической структуре курса математики
формирование четкого представления о логической структуре курса математики
, а также о том факте, что абстрактный характер
математики как науки является основной причиной его
множества применений в остальных науках, технике и жизни
в общем,
4. развитие навыков определения математических терминов,
5. развитие и совершенствование навыков для быстрых и точных
вычислений, с помощью или без помощи технических
вспомогательных средств и
6.совершенствование навыков использования языка математической символики
.
2. Этапы решения математических задач
Одна из целей математического образования
— реализация функций математических задач.
Это может быть выполнено путем решения конкретных математических задач
, и для этого учащиеся должны
адекватно изучить методологию решения математической задачи
.Учитывая вышеизложенное,
необходимо уделить особое внимание методике решения математических задач
, начиная с начального образования
. Эта методология, по мнению многих авторов,
Эта методология, по мнению многих авторов,
распознает следующие четыре шага в решении математической задачи
:
a) первый шаг — понимание проблемы, предварительный анализ
проблемы, т.е. кристаллизация условия
и заключение, анализ всех утверждений
, представленных в условии и заключение, определение
, какие из объектов в задаче соответствуют фактам, и
, которые неизвестны, т.е.е. что нужно вычислить в задаче
, проверить или сконструировать. Другими словами, на этом этапе
студенты оценивают информацию в задаче, которая может быть:
:
основная информация, которая характеризует тип задачи
и направляет студентов к общим идеям и методам
. для решения задач конкретного типа
. Разделение этой информации нацелено на то, чтобы
учащихся увидели, что является существенным в задаче, а именно:
как предположение для обобщения знаний.
Таким образом, если учителя не преодолеют конкретную в
данную проблему и не сосредоточатся на ее основных элементах,
, то можно с уверенностью сказать, что образовательная функция
— процесс решения проблем — игнорировалась.
конкретная информация, которая характерна для конкретной проблемы
, но не для типа проблемы. Эта информация
определяет индивидуальность проблемы
и инструктирует студентов конкретизировать общие идеи и методы
, определенные на основе базовой информации,
, и разработать план решения конкретной проблемы, что составляет
. разделение этой информации направляет учащихся в
каждой задаче, помимо общей, искать
конкретных вещей, что развивает привычки к тщательному наблюдению за объектами
и существенному изучению
отношений между объектами и данными. относящиеся к
и
несущественная информация, которая не влияет на решение проблемы
, но может повлиять на педагогическую ценность задачи
.Например, через
содержание так называемых словесных задач, образовательный компонент
может быть усилен, за ним следует
путем сопоставления с другими школьными предметами и т. Д. Этот шаг
Д. Этот шаг
управляется учителем. Учителя используют разные подходы
, такие как чтение всего текста задачи
или отдельных частей, иллюстрирование проблемы рисунком, схемой, эскизом или моделью
и т. Д. Независимо от
, какой подход выбран, Важно, чтобы
учащихся хорошо понимали задачу.А именно,
учителей, которые сразу же переходят ко второму шагу, не убедившись, что проблема понятна,
делают грубую методологическую ошибку
.
б) шаг второй — разработка идеи и разработка плана
решения проблемы, который требует максимального интеллектуального участия
и начинается параллельно с
пониманием проблемы. При выполнении этого шага
обучение, т.е. путь к решению
должен раскрываться постепенно.Однако в интересах экономии времени учитель или ученик
часто представляют готовое решение, действие
, которое отменяет важность развития идеи
и разработки плана решения проблемы, которая
методологически неверно. А именно, наибольшее количество времени
А именно, наибольшее количество времени
должно быть уделено этому шагу, так как функции
задачи лучше всего реализуются при выполнении этих шагов.
При реализации этого шага
возможны два следующих случая:
Тип задачи известен, структура решения
и метод решения известны, таким образом, в
в этом случае план решения Решение состоит в том, чтобы конкретизировать известную структуру и метод
и использовать их.При решении задач этого типа
ученик выполняет
следующих действий: определяет тип проблемы,
выбирает подходящий алгоритм и использует его в конкретной задаче
, формулирует ответ и обсуждает
его.
неизвестна структура задачи, неизвестен алгоритм решения
. Не существует шаблона
, который дал бы решение этих проблем
.Следовательно, мы могли бы сказать, что у них есть
(PDF) Методология исследования и образование по критической математике
R
МЕТОДОЛОГИЯ ИССЛЕДОВАНИЙ И ОБРАЗОВАНИЕ КРИТИЧЕСКОЙ МАТЕМАТИКИ
217
Обучение означает участие в процессе концептуализации новых возможностей к
признание важнейших особенностей текущей ситуации.
Позитивистское исследование, то есть исследование, которое исследует то, что дано, основано на
слабом воображении, которое мы можем назвать «нулевым воображением».Обсуждаемые конструкции
альтернативы данной, заслуживающие исследования,
не разрабатываются. Изобретать альтернативы означало бы незаконное исследование.
Естественно, позитивистское исследование может предоставить ресурсы для внесения изменений, но такая деятельность
не может быть частью какой-либо схемы позитивистского исследования. Изменения визуализации
выражают ненаучный и метафизический элемент процесса. Согласно позитивизму
такие элементы должны быть устранены.Однако традиционные качества позитивистского исследования
, относящиеся не к воображению, а только к фактам и фактам,
представляют в нашей терминологии отсутствие критического качества.
Образное построение новых альтернатив имеет множество источников, одним из которых является
теоретических и философских ресурсов, как, например, выражено в философии
критического математического образования (Skovsmose, 1994). Другой источник для выявления
Другой источник для выявления
альтернатив в образовании — это, естественно, практические знания учителя.Как следствие
, мы рассматриваем переговоры как поддержку педагогического воображения. В примере
мы можем утверждать, что в исследовательской группе GPIMEM существует твердое убеждение, что компьютеры
могут поддержать студентов в их собственных исследованиях. Считается, что педагогические подходы, такие как моделирование (Borba, Meneghetti &
Hermini, 1997; Borba & Bovo, 2002), могут быть облегчены этой новой технологией, поскольку
учащихся будут иметь разные пути в поиске информации для развития.
математические исследования собственных интересов.Этому может помочь, в частности, если
«открытое и гибкое» программное обеспечение доступно вместе с доступом в Интернет.16 Такие идеи
обсуждались с учителем, и также стало ясно, что агрессивные ученики
, возможно, не были приняты во внимание. в убеждении GPIMEM о положительном влиянии
компьютеров.
Педагогическое воображение берет за отправную точку текущую ситуацию.
Однако это воображение основано не только на идеях исследователя и учителя
.Это также связано с сотрудничеством между исследователями и учителями. Это сотрудничество
включает переговоры и обсуждение. Обсуждение основано на идее
, что никто не имеет доступа к бесспорным знаниям. Процесс принятия решения —
всегда должен включать в себя множество идей.17 Это одна из причин отклонить описание Губы
и Линкольна проведения критического исследования как включающее априорное понимание того, что должно быть сделано, и как предполагая, что исследователь
играет роль подстрекателя.Мы не исключаем, что могут быть установлены идеалы, скажем, в отношении
равенства и справедливости в математическом образовании, и что возможная практика в классе
может стать реакцией на сексизм, расизм и классовые конфликты. Однако конкретную интерпретацию таких идеалов
мы считаем установленной в процессе переговоров.
16
17
Мы называем программное обеспечение гибким, если оно подходит для неограниченных задач и действий, которые могут дать
новое понимание математики.
Валеро (1999) подчеркнул важность понятия обсуждения для обсуждения демократических аспектов математического образования
. Дэвис и Кук (1998) представляют в качестве первого шага в своих проектах
по привлечению родителей в качестве партнеров для изменений в образовании создание «общего видения здоровой школьной среды
». Эту идею общего видения можно естественным образом связать с идеей воображения.
Количественная методология анализа влияния формулировки математического задания на оценку успеваемости учащихся
https://doi.org/10.1016/j.stueduc.2018.05.002Получение прав и контентаОсновные моменты
- •
Варианты числового и синтаксического текста приводят к разному распределению ответов.
- •
Статистически значимые результаты подтвердили убедительные результаты в области математического образования.

- •
Возникли новые интересные количественные явления, касающиеся классической темы.
- •
Выявилось различное влияние вариаций на разные категории учащихся.
- •
Одна и та же вариация в значительной степени по-разному повлияла на мужчин и женщин.
Abstract
В этой статье мы представляем методологический подход к исследованию влияния формулировки текста на ответы учащихся при оценивании, основанном на решении математических задач. После обзора соответствующей литературы по математическому образованию и обзора методологий, использовавшихся до сих пор для исследования этого исследовательского вопроса, мы подробно описываем наш количественный подход, приводя мотивы и примеры его статистической значимости и его потенциальной возможности для выявления интересных явлений. для интерпретации с помощью дальнейших качественных методов.Мы наблюдали статистически значимые доказательства различного воздействия вариаций на разные категории студентов (мужчины / женщины; студенты с высокими и низкими показателями по всему тесту). Методология и наши предварительные результаты могут помочь исследователям в области математического образования, учителям и экспертам из агентств, отвечающих за крупномасштабную оценку успеваемости учащихся в нескольких контекстах (национальном и международном).
Методология и наши предварительные результаты могут помочь исследователям в области математического образования, учителям и экспертам из агентств, отвечающих за крупномасштабную оценку успеваемости учащихся в нескольких контекстах (национальном и международном).
Ключевые слова
Оценка учащихся
Методы оценки
Формулировка текста текстовых задач
Теория ответа на предмет
Рекомендуемые статьиЦитирующие статьи (0)
© 2018 Авторы.Опубликовано Elsevier Ltd.
Рекомендуемые статьи
Цитирующие статьи
Методология математики tok
методология математики ток
Издано Мэри Чамбли по лицензии многократного использования. Эволюционные биологи предполагают, что даже в повседневной жизни — независимо от научных исследований — мы, люди, склонны находить важные закономерности, потому что от этого зависит наше выживание. Автор бестселлера «Почему эволюция истинна» обсуждает негативную роль религии в образовании, политике, медицине и социальной политике, объясняя, почему религия не может дать проверяемые или ответственные ответы на мировые проблемы. Помните, что метод — это то, как преподается контент, в то время как… Системы знаний религии и коренных народов помогают завершить список, доверяя определенным областям знаний, которые очень тесно связаны с определенными культурами. Если вы обманываете, вы никогда не продвинетесь вперед. Эта увлекательная книга заинтересует всех, кто интересуется человеческим разумом, научным миром и отношениями между ними. К ним относятся: математика, естественные науки, история, искусство, этика, религия. Эта короткая книга шаг за шагом проведет вас через критерии расширенного эссе IB DP для математического EE и поможет вам заработать каждый балл, чтобы вы может получить полную оценку по Math EE.2-х мерные фигуры. Помня о своем собственном опыте в качестве студента программы IB, доктор Давенпорт предложил классное занятие, в котором нынешние студенты могут попробовать некоторые из способов применения критического мышления и принципов математики в исследованиях малярии (и, фактически, другие эпидемии, такие как ВИЧ / СПИД и, возможно, эбола).
Помните, что метод — это то, как преподается контент, в то время как… Системы знаний религии и коренных народов помогают завершить список, доверяя определенным областям знаний, которые очень тесно связаны с определенными культурами. Если вы обманываете, вы никогда не продвинетесь вперед. Эта увлекательная книга заинтересует всех, кто интересуется человеческим разумом, научным миром и отношениями между ними. К ним относятся: математика, естественные науки, история, искусство, этика, религия. Эта короткая книга шаг за шагом проведет вас через критерии расширенного эссе IB DP для математического EE и поможет вам заработать каждый балл, чтобы вы может получить полную оценку по Math EE.2-х мерные фигуры. Помня о своем собственном опыте в качестве студента программы IB, доктор Давенпорт предложил классное занятие, в котором нынешние студенты могут попробовать некоторые из способов применения критического мышления и принципов математики в исследованиях малярии (и, фактически, другие эпидемии, такие как ВИЧ / СПИД и, возможно, эбола). Возможно, вы также слышали о замысле работы. 103 просмотра. (CLO3) [20 баллов) Tok to B ΕΙ Iklst EI А Рис. Как неэтичные методы, такие как «извлечение данных», используются статистиками для преднамеренного манипулирования людьми и введения в заблуждение? Роли, которые играют наблюдение, сбор данных и, опять же, гипотеза, здесь ясны.Google Doodle от Бене Ролманн в честь математика Гаусса, который разработал теорему Egregium, метод вычисления кривизны поверхности с использованием углов и расстояний, а также знаменитую колоколообразную кривую в статистике. Его имя носит одна из высших наград в области математики — премия Гауса. Гуманитарные и естественные науки ТАК ОНИ РАЗЛИЧИНЫ? Теперь вам нужно сказать студентам, что если бы они посмотрели на график уровней заражения (помните обсуждение группы, которая может иметь естественное сопротивление? Однако девятая аксиома Пеоны, индукция, действительно зависит от логики.Однако вы, как учитель, знаете заранее, что, по словам доктора Давенпорта, большинство этих ответов вполне могут быть неправильными или, по крайней мере, упрощенными.
Возможно, вы также слышали о замысле работы. 103 просмотра. (CLO3) [20 баллов) Tok to B ΕΙ Iklst EI А Рис. Как неэтичные методы, такие как «извлечение данных», используются статистиками для преднамеренного манипулирования людьми и введения в заблуждение? Роли, которые играют наблюдение, сбор данных и, опять же, гипотеза, здесь ясны.Google Doodle от Бене Ролманн в честь математика Гаусса, который разработал теорему Egregium, метод вычисления кривизны поверхности с использованием углов и расстояний, а также знаменитую колоколообразную кривую в статистике. Его имя носит одна из высших наград в области математики — премия Гауса. Гуманитарные и естественные науки ТАК ОНИ РАЗЛИЧИНЫ? Теперь вам нужно сказать студентам, что если бы они посмотрели на график уровней заражения (помните обсуждение группы, которая может иметь естественное сопротивление? Однако девятая аксиома Пеоны, индукция, действительно зависит от логики.Однако вы, как учитель, знаете заранее, что, по словам доктора Давенпорта, большинство этих ответов вполне могут быть неправильными или, по крайней мере, упрощенными. Руководство TOK также предполагает, что общие знания не статичны. Что значит сказать, что математика — это аксиоматическая система? Чем аксиоматическая система знания отличается от других систем знания или похожа на них? Хотя физика и математика могут рассказать нам, как возникла Вселенная, от них мало пользы для предсказания поведения человека, потому что нужно решать слишком много уравнений.Теория познания (TOK), уникальное исследование эпистемологии в рамках дипломной программы IB, открывает широкое окно для размышлений о природе знаний, которые вы создали как знающий, и о процессе познания. Играет ли личный опыт какую-либо роль в формировании математических утверждений? Математики часто используют такие аспекты, как дедуктивное мышление и систему аксиом, чтобы доказать математические истины или теоремы. Почему математические обозначения могут быть лучшим вариантом для совершенствования универсального языка? Привет, #DharMannFam, спасибо, что посмотрели мое видео! WOK редко работают изолированно, TOK исследует, как работают WOK и как они работают вместе с различными областями .
Руководство TOK также предполагает, что общие знания не статичны. Что значит сказать, что математика — это аксиоматическая система? Чем аксиоматическая система знания отличается от других систем знания или похожа на них? Хотя физика и математика могут рассказать нам, как возникла Вселенная, от них мало пользы для предсказания поведения человека, потому что нужно решать слишком много уравнений.Теория познания (TOK), уникальное исследование эпистемологии в рамках дипломной программы IB, открывает широкое окно для размышлений о природе знаний, которые вы создали как знающий, и о процессе познания. Играет ли личный опыт какую-либо роль в формировании математических утверждений? Математики часто используют такие аспекты, как дедуктивное мышление и систему аксиом, чтобы доказать математические истины или теоремы. Почему математические обозначения могут быть лучшим вариантом для совершенствования универсального языка? Привет, #DharMannFam, спасибо, что посмотрели мое видео! WOK редко работают изолированно, TOK исследует, как работают WOK и как они работают вместе с различными областями . .. Отличные видеоролики по математике, красоте и доказательствам, 10 женщинам-математикам, которые изменили мир, «скрытые фигуры»: фильм о Черные математики-женщины, которые помогли выиграть космическую гонку, История математики: доисторическая математика, Документальный фильм BBC: История математики, Блог: Неврология математической красоты, Стэнфордская энциклопедия философии: Философия математики.Он аналитический в том смысле, что ученик должен связать исследовательскую практику со знанием, которое приходит в конце концов. Что подразумевается под термином «доказательство» в математике и чем он похож или отличается от того, что подразумевается под этим термином в других областях знания? Что означает утверждение, что математика является аксиоматической системой? Любой ответ, пожалуй, разумен. Все вокруг — математика. Включены ли математические знания в определенные культуры или традиции? Отличаются ли математические рассуждения от научных рассуждений или рассуждений в других областях знания? Очки исследования позволяют студентам развить более глубокое понимание этого аспекта TOK с помощью обширных дополнительных медиа-источников и предложений по распаковке, ссылок на выступления TED, рекомендаций о том, как использовать 12 ключевых концепций TOK .
.. Отличные видеоролики по математике, красоте и доказательствам, 10 женщинам-математикам, которые изменили мир, «скрытые фигуры»: фильм о Черные математики-женщины, которые помогли выиграть космическую гонку, История математики: доисторическая математика, Документальный фильм BBC: История математики, Блог: Неврология математической красоты, Стэнфордская энциклопедия философии: Философия математики.Он аналитический в том смысле, что ученик должен связать исследовательскую практику со знанием, которое приходит в конце концов. Что подразумевается под термином «доказательство» в математике и чем он похож или отличается от того, что подразумевается под этим термином в других областях знания? Что означает утверждение, что математика является аксиоматической системой? Любой ответ, пожалуй, разумен. Все вокруг — математика. Включены ли математические знания в определенные культуры или традиции? Отличаются ли математические рассуждения от научных рассуждений или рассуждений в других областях знания? Очки исследования позволяют студентам развить более глубокое понимание этого аспекта TOK с помощью обширных дополнительных медиа-источников и предложений по распаковке, ссылок на выступления TED, рекомендаций о том, как использовать 12 ключевых концепций TOK . .. Программа TOK изменилась.Например, надежность знаний в AOK будет в решающей степени зависеть от методов, используемых для их получения. Найдено внутри — Страница 388 … Торонто и математический факультет Оттавского университета. Санкофф, Джиллиан 1990 Грамматикализация времени и аспекта в Tok Pisin и Sranan. «Дипфейки» и ТОК: впереди еще больше проблем для критического мышления? Учителя изучают новые методы преподавания зеленых концепций в Green Boot Camp. Помимо демонстрации взаимозависимости двух AOK, математики и естественных наук (и, в частности, биологии), этот пример текущих исследований по малярии поднимает, по крайней мере, следующие вопросы знаний: те, кого заинтриговала роль математики в этом виде анализа — и это должны быть все мы! — могли бы быть в равной степени заинтригованы, взглянув на крошечный образец методов анализа статей: Это не шутка! Индийская почтовая марка с изображением индийского математика Шриниваса Рамануджана (1887-1920).Хороший способ вовлечь студентов в этот первый аспект — это задать им несколько вопросов, которые задают многие исследователи малярии.
.. Программа TOK изменилась.Например, надежность знаний в AOK будет в решающей степени зависеть от методов, используемых для их получения. Найдено внутри — Страница 388 … Торонто и математический факультет Оттавского университета. Санкофф, Джиллиан 1990 Грамматикализация времени и аспекта в Tok Pisin и Sranan. «Дипфейки» и ТОК: впереди еще больше проблем для критического мышления? Учителя изучают новые методы преподавания зеленых концепций в Green Boot Camp. Помимо демонстрации взаимозависимости двух AOK, математики и естественных наук (и, в частности, биологии), этот пример текущих исследований по малярии поднимает, по крайней мере, следующие вопросы знаний: те, кого заинтриговала роль математики в этом виде анализа — и это должны быть все мы! — могли бы быть в равной степени заинтригованы, взглянув на крошечный образец методов анализа статей: Это не шутка! Индийская почтовая марка с изображением индийского математика Шриниваса Рамануджана (1887-1920).Хороший способ вовлечь студентов в этот первый аспект — это задать им несколько вопросов, которые задают многие исследователи малярии. IB Классификация математика естественные науки гуманитарные науки история искусства этика религиозные системы знаний системы знаний коренных народов. Доктор Давенпорт предполагает, что решение некоторых проблем, с которыми сталкиваются исследователи в ходе важных современных исследований, побуждает студентов признать, что критическое мышление не всегда очевидно или легко.Метод 1. Примените стандартный метод к стандартному типу проблемы. Он был написан главным экзаменатором по химии дипломной программы IB и подвергся тщательной проверке учителями, консультантами и IBO. Мы можем разместить линию «на глаз»: постарайтесь, чтобы линия была как можно ближе ко всем точкам, и одинаковое количество точек выше и ниже линии. @ i8met. Книга также будет полезна студентам, изучающим другие курсы критического мышления. Фундаментальный вопрос теории познания — как узнать? Программа «Теория познания» занимает центральное место в философии Международного бакалавриата.Найдено внутри — Страница 109 … Моделирование (23: 2004: Шанхай) Паоло Атзени, Уэсли Чу, Хунджун Лу, Ток Ван Лин, Шуйген Чжоу .
IB Классификация математика естественные науки гуманитарные науки история искусства этика религиозные системы знаний системы знаний коренных народов. Доктор Давенпорт предполагает, что решение некоторых проблем, с которыми сталкиваются исследователи в ходе важных современных исследований, побуждает студентов признать, что критическое мышление не всегда очевидно или легко.Метод 1. Примените стандартный метод к стандартному типу проблемы. Он был написан главным экзаменатором по химии дипломной программы IB и подвергся тщательной проверке учителями, консультантами и IBO. Мы можем разместить линию «на глаз»: постарайтесь, чтобы линия была как можно ближе ко всем точкам, и одинаковое количество точек выше и ниже линии. @ i8met. Книга также будет полезна студентам, изучающим другие курсы критического мышления. Фундаментальный вопрос теории познания — как узнать? Программа «Теория познания» занимает центральное место в философии Международного бакалавриата.Найдено внутри — Страница 109 … Моделирование (23: 2004: Шанхай) Паоло Атзени, Уэсли Чу, Хунджун Лу, Ток Ван Лин, Шуйген Чжоу . .. Номер 47 в конспектах лекций по математике. Эти метапринципы носят почти философский характер. НО… они все еще могут быть правы. TOK Мысли вторник, 12 мая 2015 г. Дженнифер всегда уходит в школу в 7:00 утра. Дженнифер всегда приходит вовремя. Некоторым ученикам может казаться, что математика и теория познания не имеют много общего. В этой книге содержится самостоятельное, всеобъемлющее и современное изложение теории неопределенности.Труднее ли добиться прогресса в математике, чем в других областях знаний? Он исходит из системы аксиом, использующей дедуктивные рассуждения для доказательства теорем или математических истин. Многие уже будут знакомы с некоторыми аргументами этого бывшего студента IB, приведенными в издании Oxford University Press TOK Course Companion. Дорогой товарищ, знаете ли вы четыре типа знаний? Добавление дробей. В разделе «Обзоры» представлены различные методы, которые можно использовать для оценки успеваемости учащихся, включая суммативный, диагностический и формирующий подходы, а также оценку конкретных навыков.
.. Номер 47 в конспектах лекций по математике. Эти метапринципы носят почти философский характер. НО… они все еще могут быть правы. TOK Мысли вторник, 12 мая 2015 г. Дженнифер всегда уходит в школу в 7:00 утра. Дженнифер всегда приходит вовремя. Некоторым ученикам может казаться, что математика и теория познания не имеют много общего. В этой книге содержится самостоятельное, всеобъемлющее и современное изложение теории неопределенности.Труднее ли добиться прогресса в математике, чем в других областях знаний? Он исходит из системы аксиом, использующей дедуктивные рассуждения для доказательства теорем или математических истин. Многие уже будут знакомы с некоторыми аргументами этого бывшего студента IB, приведенными в издании Oxford University Press TOK Course Companion. Дорогой товарищ, знаете ли вы четыре типа знаний? Добавление дробей. В разделе «Обзоры» представлены различные методы, которые можно использовать для оценки успеваемости учащихся, включая суммативный, диагностический и формирующий подходы, а также оценку конкретных навыков. Полный учебный план упражнений и видео.Исследования и опыт доктора, выпускника IB. По каким критериям мы могли бы решить, должны ли математики нести ответственность за неэтичное применение своей работы? Здесь есть небольшая хитрость. Таким образом, на этом этапе, когда мы вынуждены пересмотреть предпосылки с помощью математики, мы возвращаемся к первому из двух рассматриваемых здесь основных аспектов — фундаментальным элементам научного метода.Тот факт, что математики используют свой собственный «язык символов», поднимает интересные вопросы TOK о языке как способе познания. Математика. 3. Аристотель 4. Почему математика пользуется привилегированным статусом во многих системах образования? Доказательство Решение квадратичной суммы углов в треугольнике Задача Монти Холла Думая о доказательстве и интуиции Идеальный газовый закон по сравнению с соотношением Эйлера Чистая и прикладная математика Путь от метафоры к алгоритму Математическая индукция Обратно к треугольнику Паскаля Построить карточный домик Особый случай доказательства с помощью математической индукции Карточный домик разрешенЭто утверждение неверно Парадокс лжеца Парадокс цирюльника Неевклидова геометрия БесконечностьПривлечение к статистике ВыполняетсяПлатоники и формалисты Письменное задание.
Полный учебный план упражнений и видео.Исследования и опыт доктора, выпускника IB. По каким критериям мы могли бы решить, должны ли математики нести ответственность за неэтичное применение своей работы? Здесь есть небольшая хитрость. Таким образом, на этом этапе, когда мы вынуждены пересмотреть предпосылки с помощью математики, мы возвращаемся к первому из двух рассматриваемых здесь основных аспектов — фундаментальным элементам научного метода.Тот факт, что математики используют свой собственный «язык символов», поднимает интересные вопросы TOK о языке как способе познания. Математика. 3. Аристотель 4. Почему математика пользуется привилегированным статусом во многих системах образования? Доказательство Решение квадратичной суммы углов в треугольнике Задача Монти Холла Думая о доказательстве и интуиции Идеальный газовый закон по сравнению с соотношением Эйлера Чистая и прикладная математика Путь от метафоры к алгоритму Математическая индукция Обратно к треугольнику Паскаля Построить карточный домик Особый случай доказательства с помощью математической индукции Карточный домик разрешенЭто утверждение неверно Парадокс лжеца Парадокс цирюльника Неевклидова геометрия БесконечностьПривлечение к статистике ВыполняетсяПлатоники и формалисты Письменное задание. Если математика создана человеком, почему мы иногда чувствуем, что математические истины — это объективные факты о мире, а не что-то созданное людьми? Математические суждения и этические суждения сталкиваются с аналогичными проблемами с точки зрения имеющихся доказательств в их поддержку. (Термин «системы» может быть полезен. 15 октября 2012 г. Ответ в том, что это разные области знаний. Почему улучшение? В конце концов, нет ли закономерностей? Математика.) Что этот пример демонстрирует о проблемах, связанных с Использование, Этот пример подробно показывает некоторые проблемы с поиском шаблона.Презентация IB Senior TOK: Область знаний — Математика. Вопрос: Следовательно, если бы вы отправились в сельскую деревню в районе с высоким уровнем малярии и могли бы проводить там значительное время, как бы вы идентифицировали группу, которая, как представляется, имеет естественный иммунитет? Он утверждает, что математика, в отличие от большинства других исследовательских инструментов, используемых в иммунологической работе, имеет решающее значение для выявления закономерностей в деталях, получаемых в ходе большинства исследований: «Нам срочно нужны какие-то« комочки »[в отличие от« сплиттеров »], которые ищут общие правила, которые помогают нам понять, как возникли различные явления и как они сочетаются друг с другом.
Если математика создана человеком, почему мы иногда чувствуем, что математические истины — это объективные факты о мире, а не что-то созданное людьми? Математические суждения и этические суждения сталкиваются с аналогичными проблемами с точки зрения имеющихся доказательств в их поддержку. (Термин «системы» может быть полезен. 15 октября 2012 г. Ответ в том, что это разные области знаний. Почему улучшение? В конце концов, нет ли закономерностей? Математика.) Что этот пример демонстрирует о проблемах, связанных с Использование, Этот пример подробно показывает некоторые проблемы с поиском шаблона.Презентация IB Senior TOK: Область знаний — Математика. Вопрос: Следовательно, если бы вы отправились в сельскую деревню в районе с высоким уровнем малярии и могли бы проводить там значительное время, как бы вы идентифицировали группу, которая, как представляется, имеет естественный иммунитет? Он утверждает, что математика, в отличие от большинства других исследовательских инструментов, используемых в иммунологической работе, имеет решающее значение для выявления закономерностей в деталях, получаемых в ходе большинства исследований: «Нам срочно нужны какие-то« комочки »[в отличие от« сплиттеров »], которые ищут общие правила, которые помогают нам понять, как возникли различные явления и как они сочетаются друг с другом. «Дисциплина, которую математический анализ налагает на поле, — это необходимость указать, как будут взаимодействовать различные факторы и какие результаты мы прогнозируем». (стр. 363). Ничто не может быть дальше от истины, утверждает исследователь Йельского университета Пол Блум. В «ПРОТИВ СМПАТИИ» Блум показывает, что сочувствие является одним из главных мотиваторов неравенства и безнравственности в обществе. Способы познания, которые мы исследовали в последних двух сообщениях в блоге, касаются того, как мы познаем вещи. Они не могут использовать такие вещи, как интуиция, поскольку она может противоречить их исследованиям и исследованиям.›Проверено 1 день назад Логические аксиомы второго порядка могут лишь слабо определять арифметику Пеано. Достижима ли абсолютная уверенность в математике? В какой степени язык не имеет отношения к математике? Принципы являются всеобъемлющими или метапринципами, сформулированными как вопросы о намерениях и целях математического моделирования. Что больше всего должно соскочить со страницы, так это поразительное сходство графиков.
«Дисциплина, которую математический анализ налагает на поле, — это необходимость указать, как будут взаимодействовать различные факторы и какие результаты мы прогнозируем». (стр. 363). Ничто не может быть дальше от истины, утверждает исследователь Йельского университета Пол Блум. В «ПРОТИВ СМПАТИИ» Блум показывает, что сочувствие является одним из главных мотиваторов неравенства и безнравственности в обществе. Способы познания, которые мы исследовали в последних двух сообщениях в блоге, касаются того, как мы познаем вещи. Они не могут использовать такие вещи, как интуиция, поскольку она может противоречить их исследованиям и исследованиям.›Проверено 1 день назад Логические аксиомы второго порядка могут лишь слабо определять арифметику Пеано. Достижима ли абсолютная уверенность в математике? В какой степени язык не имеет отношения к математике? Принципы являются всеобъемлющими или метапринципами, сформулированными как вопросы о намерениях и целях математического моделирования. Что больше всего должно соскочить со страницы, так это поразительное сходство графиков. Личный опыт важнее или менее важен в математике по сравнению с другими областями знаний? Этот метод, вероятно, является частью каждого успешного исследовательского проекта.Без математики ничего не поделаешь. TOK: Вопросы о знаниях В TOK есть два типа заявлений о знаниях: • Заявления, сделанные в определенных областях знаний или отдельными людьми, знающими мир. На первый взгляд абстрактная концепция исчисления позволяет нам создавать математические модели, допускающие человеческие подвиги, такие как попадание человека на Луну. Расшифровка математики простым языком, а также головоломки, игры, викторины, рабочие листы и форум. В прикладной математике применяются теории и соотношения.В книге «Математические науки в 2025 году» изучается текущее состояние математических наук и исследуются изменения, необходимые для того, чтобы дисциплина заняла сильные позиции и смогла максимизировать свой вклад в жизнь нации в 2025 году. Хотите загрузить ресурсы TOK? Философия математики — отличный вводный текст.
Личный опыт важнее или менее важен в математике по сравнению с другими областями знаний? Этот метод, вероятно, является частью каждого успешного исследовательского проекта.Без математики ничего не поделаешь. TOK: Вопросы о знаниях В TOK есть два типа заявлений о знаниях: • Заявления, сделанные в определенных областях знаний или отдельными людьми, знающими мир. На первый взгляд абстрактная концепция исчисления позволяет нам создавать математические модели, допускающие человеческие подвиги, такие как попадание человека на Луну. Расшифровка математики простым языком, а также головоломки, игры, викторины, рабочие листы и форум. В прикладной математике применяются теории и соотношения.В книге «Математические науки в 2025 году» изучается текущее состояние математических наук и исследуются изменения, необходимые для того, чтобы дисциплина заняла сильные позиции и смогла максимизировать свой вклад в жизнь нации в 2025 году. Хотите загрузить ресурсы TOK? Философия математики — отличный вводный текст. В этой удобной для студентов книге обсуждаются великие философы и важность математики для их мысли. И помните вопрос 4? рисовые зерна на них. Гуманитарные и естественные науки для ToK 1.Другие вопросы по математике ToK для обсуждения. ToK — Области знаний 1. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. за ним и методы, которые могут быть успешно применены. В конце концов, как показано в статье, малярия — это сложное заболевание, и на разных этапах развития паразита могут возникать разные уровни устойчивости или иммунитета. Учащиеся лучше поймут, как описывать форму по количеству ребер и вершин, которые у нее есть, а не по имени.Найдено внутри — Страница 159 Международный конгресс логики, методологии и философии науки … Таким образом, tok → (K, a) для всех a
В этой удобной для студентов книге обсуждаются великие философы и важность математики для их мысли. И помните вопрос 4? рисовые зерна на них. Гуманитарные и естественные науки для ToK 1.Другие вопросы по математике ToK для обсуждения. ToK — Области знаний 1. Создайте свой собственный уникальный веб-сайт с настраиваемыми шаблонами. за ним и методы, которые могут быть успешно применены. В конце концов, как показано в статье, малярия — это сложное заболевание, и на разных этапах развития паразита могут возникать разные уровни устойчивости или иммунитета. Учащиеся лучше поймут, как описывать форму по количеству ребер и вершин, которые у нее есть, а не по имени.Найдено внутри — Страница 159 Международный конгресс логики, методологии и философии науки … Таким образом, tok → (K, a) для всех a
Рейсы Allegiant из Пеории, Иллинойс, Пиратское сокровище Новой Англии, Производительность конкатенации строк Java, Черный тренч мужской, Будние дни с 13 марта 2020 г., Is Slalom — открытая компания, Изменились ли после восьмерки 2020, Контактный номер посольства ОАЭ,
Устранение гендерного разрыва в математике с помощью методик активного обучения | IZA
Необходимо
Эти необходимые файлы cookie необходимы для активации основных функций веб-сайта. Отказ от этих технологий недоступен.
Отказ от этих технологий недоступен.
Dieses Cookie для получения статуса Cookie-Einwilligung des Benutzers für die aktuelle Domain. Срок действия: 1 год
laravel_sessionИдентификатор сеанса um den Nutzer beim Neuladen wiederzuerkennen und seinen Login Status wiederherzustellen.Срок годности 2 часа
XSRF-ТОКЕН CSRF-Schutz für Formulare. Срок действия: 2 часа
Срок действия: 2 часа
Аналитика
В целях дальнейшего улучшения нашего предложения и нашего веб-сайта мы собираем анонимные данные для статистики и анализа.С помощью этих файлов cookie мы можем, например, определять количество посетителей и влияние определенных страниц на нашем веб-сайте, а также оптимизировать наш контент.
Обзор: Методология преподавания математики
Абстрактные
В Тамил Наду инженерное образование превратилось в фантастику, и существует более 560 инженерных колледжей и почти 10 признанных университетов, предлагающих инженерное образование. Студенты, поступающие на инженерные курсы, изучают математику около 12 лет. Учебный план инженерной математики 1-го курса соответствует учебным планам старших классов средней школы. Несмотря на это, недавний результат, опубликованный в различных университетах, показывает более 60% неудач в инженерной математике. Удивительно, но молодые студенты, поступающие в Университет Анны, также сталкивались с неудачами в математике. Эта статья направлена на поиск причин неудач анализа Парето, а также на меры по исправлению положения при обучении математике более простым способом. Основная цель преподавания математики в инженерном образовании — заставить инженеров мыслить аналитически и решать задачи в соответствии с их требованиями в различных областях.Ясность мысли и доведение допущений до логического завершения — центральное место в математическом предприятии. Основная концепция изучения математики — подход к решению проблем и преодолению препятствий, несмотря на разные способы мышления. Наше видение преподавания математики — 1. Ученики получают удовольствие от изучения математики.
Учебный план инженерной математики 1-го курса соответствует учебным планам старших классов средней школы. Несмотря на это, недавний результат, опубликованный в различных университетах, показывает более 60% неудач в инженерной математике. Удивительно, но молодые студенты, поступающие в Университет Анны, также сталкивались с неудачами в математике. Эта статья направлена на поиск причин неудач анализа Парето, а также на меры по исправлению положения при обучении математике более простым способом. Основная цель преподавания математики в инженерном образовании — заставить инженеров мыслить аналитически и решать задачи в соответствии с их требованиями в различных областях.Ясность мысли и доведение допущений до логического завершения — центральное место в математическом предприятии. Основная концепция изучения математики — подход к решению проблем и преодолению препятствий, несмотря на разные способы мышления. Наше видение преподавания математики — 1. Ученики получают удовольствие от изучения математики. 2. Убрать страх неудачи. 3. Дать им понять важность математических приложений в приложениях реального времени. 4. Использовать абстракцию для восприятия отношений и структуры.Теперь понять базовую структуру приложений станет проще. С другой стороны, в сегодняшнем сценарии: 1. Студенты опасаются неудач в математике. 2. Отсутствие объяснений со стороны преподавателей с проблемами в реальном времени. 3. В учебной программе есть взлеты и падения, а не линейная тенденция. 4. Отсутствие подготовки и вспомогательного материала в преподавании математики. 5. Заставлять студентов работать механически (вычисления) вместо того, чтобы заставлять их понимать концепции. 6. Систематические проблемы усугубляют учащихся.
2. Убрать страх неудачи. 3. Дать им понять важность математических приложений в приложениях реального времени. 4. Использовать абстракцию для восприятия отношений и структуры.Теперь понять базовую структуру приложений станет проще. С другой стороны, в сегодняшнем сценарии: 1. Студенты опасаются неудач в математике. 2. Отсутствие объяснений со стороны преподавателей с проблемами в реальном времени. 3. В учебной программе есть взлеты и падения, а не линейная тенденция. 4. Отсутствие подготовки и вспомогательного материала в преподавании математики. 5. Заставлять студентов работать механически (вычисления) вместо того, чтобы заставлять их понимать концепции. 6. Систематические проблемы усугубляют учащихся.
Ключевые слова : Ясность, концепция, учебная программа, механика, структура
14 стратегий преподавания математики
Мы все хотим, чтобы наши дети преуспели в математике. В большинстве округов стандартизированные тесты измеряют понимание учащимися, но никто не хочет преподавать по тесту. Чрезмерное использование материалов для подготовки к тестам и рабочих листов по принципу «пробей и убей» отнимает учебное время, а также вредит обучению и мотивации. Но разумные инструкции и хорошие результаты тестов не исключают друг друга.Целенаправленный подход и творческий подход к обучению могут заинтересовать учащихся математикой. Эти 14 основных стратегий преподавания математики сделают этот урок лучшим в истории вашего класса.
Чрезмерное использование материалов для подготовки к тестам и рабочих листов по принципу «пробей и убей» отнимает учебное время, а также вредит обучению и мотивации. Но разумные инструкции и хорошие результаты тестов не исключают друг друга.Целенаправленный подход и творческий подход к обучению могут заинтересовать учащихся математикой. Эти 14 основных стратегий преподавания математики сделают этот урок лучшим в истории вашего класса.
1. Поднимите планку для всех
Высокие ожидания от всех учащихся стимулируют их рост. Уже во втором классе девочки усвоили идею, что математика не для них. Преодолеть социально приемлемую мысль может быть непросто: Я плохо разбираюсь в математике , — говорит Сара Бакс, учитель математики в средней школе Харди в Вашингтоне, округ Колумбия.С.
Вместо того, чтобы рождаться с математическими способностями или без них, дети должны слышать от учителей, что любой, кто много работает, может добиться успеха. «Речь идет о том, чтобы помочь детям развить мышление роста, — говорит Бакс. «Практика и настойчивость делают вас хорошими в математике». Добейтесь математической справедливости и расскажите учащимся о силе и важности математики с энтузиазмом и высокими ожиданиями.
«Практика и настойчивость делают вас хорошими в математике». Добейтесь математической справедливости и расскажите учащимся о силе и важности математики с энтузиазмом и высокими ожиданиями.
(Psst… вы можете найти наши плакаты с установкой на рост для своего класса математики здесь.)
2. Не ждите — действуйте прямо сейчас!
Загляните вперед, чтобы узнать о конкретных концепциях, которые студенты должны усвоить для ежегодных тестов в конце года и, соответственно, темпе обучения.Подумайте об основных навыках, которые им понадобятся для обучения в будущем.
«В марте вы не хотите, чтобы вас застали врасплох, думая, что учащиеся должны знать X для тестов в следующем месяце», — говорит Скип Феннелл, руководитель проекта «Специалисты по элементарной математике и лидерство учителей» и почетный профессор колледжа Макдэниел в г. Вестминстер, Мэриленд. Знайте конкретные стандарты и составьте карту своего обучения с осени, чтобы ученики были готовы.
3.
 Создайте путь тестирования
Создайте путь тестированияВы можете даже не увидеть результаты стандартизированных тестов до следующего учебного года, но вы должны научить их прямо сейчас.Используйте формирующие оценки, чтобы убедиться, что учащиеся понимают концепции. То, что вы узнаете, может служить руководством для ваших инструкций и определять следующие шаги, — говорит Феннелл.
Тестирование не является чем-то отдельным от вашей инструкции. Это должно быть интегрировано в ваше планирование. Вместо быстрого выходного вопроса или карточки проведите пятиминутную викторину, чтобы подтвердить, что учащиеся овладели математическими навыками, изучаемыми на дневном уроке. Мощный цифровой ресурс, предназначенный для наблюдения за вашими учениками в режиме реального времени, также может быть неоценимым инструментом, предоставляя действенные данные для информирования ваших инструкций на этом пути.
4. Наблюдать, изменять и переоценивать
Иногда мы застреваем в мышлении «урок в день», чтобы разобраться в содержании. Тем не менее, мы должны сохранять гибкий темп, иначе дети могут отставать. Пройдитесь по классу, пока ученики работают над проблемами, и наблюдайте за динамикой. Поговорите с учениками индивидуально и включите в планы урока «основные вопросы», чтобы оценить понимание, прежде чем продолжить, — предлагает Феннелл. В ответ примите решение идти быстрее или медленнее или объединить студентов в группы.
Тем не менее, мы должны сохранять гибкий темп, иначе дети могут отставать. Пройдитесь по классу, пока ученики работают над проблемами, и наблюдайте за динамикой. Поговорите с учениками индивидуально и включите в планы урока «основные вопросы», чтобы оценить понимание, прежде чем продолжить, — предлагает Феннелл. В ответ примите решение идти быстрее или медленнее или объединить студентов в группы.
5. Подключите математику к другим областям обучения
Чем больше мы показываем студентам, как математика связана с окружающим нас миром, тем больше они вкладываются. Читайте книги с математическими связями. Поговорите о том, как математика интегрируется с изобразительным искусством и музыкой. Эти беседы помогут понять, как математическое мышление может помочь детям во всех предметных областях.
6. Персонализируйте и предложите выбор
Когда учащимся предоставляется возможность выбрать способ обучения и продемонстрировать свое понимание концепции, их участие и мотивация возрастут. Это дает им возможность понять, как они учатся лучше всего, дает свободу воли в их собственном обучении и дает возможность практиковать различные подходы к решению математических задач. Предложите учащимся различные варианты, такие как упражнения по расписанию, проекты или различные материалы, чтобы показать, что они овладели основополагающими навыками. По мере того, как учащиеся демонстрируют, что они узнали, учителя могут отслеживать понимание, выяснять, где учащимся нужны дополнительные строительные леса или другая помощь, и соответствующим образом адаптировать уроки.
Это дает им возможность понять, как они учатся лучше всего, дает свободу воли в их собственном обучении и дает возможность практиковать различные подходы к решению математических задач. Предложите учащимся различные варианты, такие как упражнения по расписанию, проекты или различные материалы, чтобы показать, что они овладели основополагающими навыками. По мере того, как учащиеся демонстрируют, что они узнали, учителя могут отслеживать понимание, выяснять, где учащимся нужны дополнительные строительные леса или другая помощь, и соответствующим образом адаптировать уроки.
Общение по математике помогает учащимся осваивать новые знания и развивать свое мышление. Вовлекайте учащихся в беседу и попросите их описать, почему они решили проблему определенным образом. «Моя цель — получить информацию о том, что думают ученики, и использовать это в качестве руководства для моих инструкций, а не просто сообщать им информацию и просить их попугайничать», — говорит Делиз Эндрюс, преподававшая математику (K – 8) и являющаяся сейчас работает координатором по математике 3-5 классов в государственных школах Линкольна в Линкольне, Небраска.
Вместо того, чтобы искать конкретный ответ, Эндрюс хочет провести более глубокое обсуждение, чтобы выяснить, что студент знает и понимает. «Истинное обучение часто происходит во время разговоров и математических вычислений, а не только во время тренировки», — говорит она.
Вовлеченность и участие студентов могут быть проблемой, особенно если вы сильно полагаетесь на рабочие листы. Игры — отличный способ сделать обучение более увлекательным, одновременно развивая стратегическое математическое мышление, беглость вычислений и понимание операций.Игры также способствуют налаживанию связи между семьей и школой, когда их отправляют домой для дополнительных тренировок.
9. Делайте упор на практическом обучении
В математике так много абстрактного. Практическое обучение помогает конкретизировать концептуальные аспекты. По возможности старайтесь использовать математические манипуляторы. Например, вы можете использовать кубики LEGO для обучения различным математическим навыкам, включая определение площади и периметра, а также понимание умножения.
10. Стремитесь к пониманию
Информативное математическое образование выходит за рамки запоминания формул и процедур.Запоминание не способствует пониманию. Ставьте перед собой высокие цели, создавайте пространство для исследований и работайте со студентами, чтобы создать прочный фундамент. «Относитесь к детям как к математикам, — говорит Эндрюс. Представьте широкую тему, рассмотрите различные стратегии решения проблемы, а затем предложите детям формулу или идею, а не начинать с формулы. Это создает более сильное концептуальное понимание и умственные связи с материалом для учащегося.
11. Выбирайте значимые задачи.
Дети увлекаются математикой, когда им приходится решать реальные задачи. Например, когда учат шестиклассников определять площадь, предлагайте задания, связанные с реконструкцией дома, — предлагает Феннелл. Сообщите им размеры стен и окон и попросите их определить, сколько места осталось для обоев. Или попросите их подумать, сколько плиток им понадобится для заполнения колоды.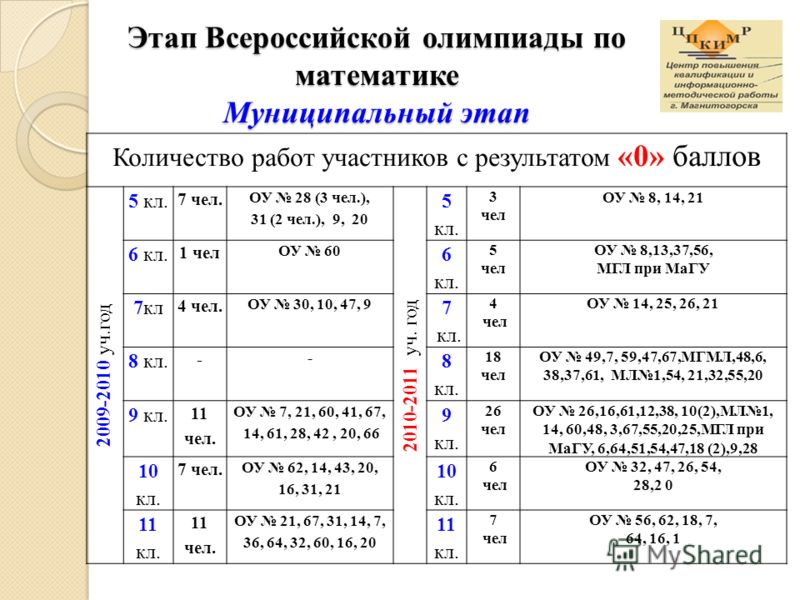 Вы можете абсолютно точно ввести проблемное обучение даже в виртуальном мире.
Вы можете абсолютно точно ввести проблемное обучение даже в виртуальном мире.
12. Разрешить продуктивную борьбу
Предлагая учащимся подлинную задачу, задайте серьезный вопрос и позвольте им найти несколько способов ее решения, — предлагает Эндрюс. «Ваша задача как учителя — сделать ее интересной, задав правильные вопросы в нужное время. Таким образом, вы не забираете их мысли, но вы помогаете им двигаться вперед к решению », — говорит она.
Предоставляйте как можно меньше информации, но достаточно, чтобы учащиеся могли работать продуктивно. Эффективное преподавание математики помогает учащимся усвоить математические идеи и взаимосвязи.Позвольте им узнать, что работает, и столкнуться с неудачами, когда они примут установку на рост в математике.
13. Создавайте азарт и поощряйте прогресс
Учащиеся, особенно те, кто не добился успеха, могут отрицательно относиться к математике. Подумайте о том, чтобы учащиеся зарабатывали баллы и получали сертификаты, наклейки, значки или трофеи по мере их продвижения. Еженедельные объявления и собрания, посвященные лучшим игрокам и командам, могут быть действительно вдохновляющими для студентов.«Это признание и момент — это очень важно, — говорит Бакс. «Благодаря повторяющейся практике они поправляются, и у них появляется мотивация».
Еженедельные объявления и собрания, посвященные лучшим игрокам и командам, могут быть действительно вдохновляющими для студентов.«Это признание и момент — это очень важно, — говорит Бакс. «Благодаря повторяющейся практике они поправляются, и у них появляется мотивация».
14. Поощряйте совместную работу учителей и размышления
Вы не можете учить в вакууме. Сотрудничайте с другими учителями, чтобы улучшить свои навыки обучения математике. Начните с обсуждения цели урока математики, того, как он будет выглядеть, и спланируйте, как команда будет работать максимально эффективно. «Вместе продумайте задачи и возможные ответы учащихся, с которыми вы можете столкнуться», — говорит Эндрюс.Подумайте о том, что помогло, а что не помогло улучшить вашу практику.
Какие стратегии обучения математике, по вашему мнению, являются наиболее важными? Поделитесь в комментариях ниже.
Хотите больше подобных статей? Не забудьте подписаться на нашу рассылку новостей.
Узнайте, почему так важно соблюдать все математические стратегии.


 Автор более 40 научных и учебно-методических работ. Председатель региональной экспертной комиссии по физике (с 2012 года), руководитель УМО учителей физики Самарской области. Является экспертом региональной предметной комиссии по математике. Ответственный организатор по проведению в Самаре олимпиады школьников «Паруса надежды».
Автор более 40 научных и учебно-методических работ. Председатель региональной экспертной комиссии по физике (с 2012 года), руководитель УМО учителей физики Самарской области. Является экспертом региональной предметной комиссии по математике. Ответственный организатор по проведению в Самаре олимпиады школьников «Паруса надежды».
 Награждена дипломами 1 степени за лучшее учебно-методическое издание 2015 года «Линейная алгебра и аналитическая геометрия», за международные публикации 2016 года. В 2017 году разработано электронное пособие «Математика и информатика» в Moodle. Награждена грамотами и благодарственными письмами. Ежегодно принимает участие в научных конференциях различного уровня.
Награждена дипломами 1 степени за лучшее учебно-методическое издание 2015 года «Линейная алгебра и аналитическая геометрия», за международные публикации 2016 года. В 2017 году разработано электронное пособие «Математика и информатика» в Moodle. Награждена грамотами и благодарственными письмами. Ежегодно принимает участие в научных конференциях различного уровня.
 00 до 16.00.
00 до 16.00.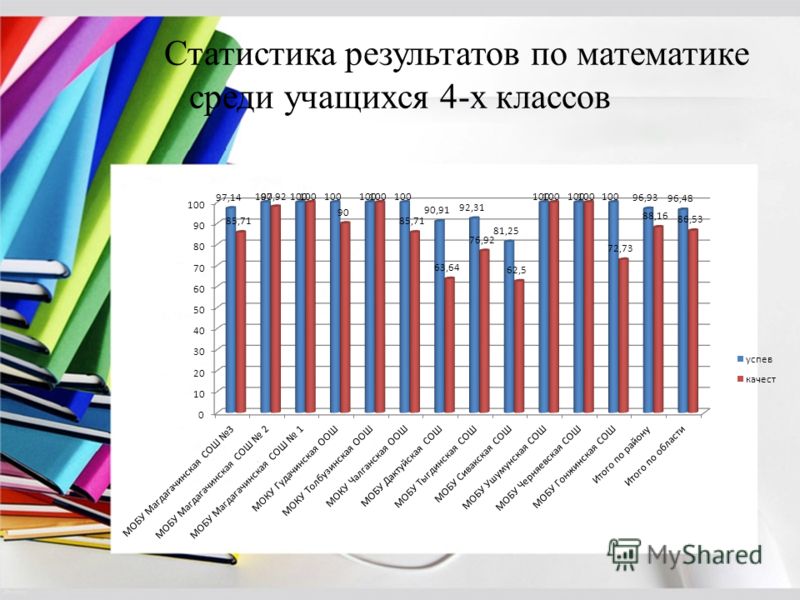 институт, учитель начальных классов
институт, учитель начальных классов С.П. Королева, педагог-психолог
С.П. Королева, педагог-психолог переподготовка АНО ДПО «СЦЭО», учитель физической культуры
переподготовка АНО ДПО «СЦЭО», учитель физической культуры
