Как делается сложный план: Сложный план текста – пример

как составить сложный план? — Школьные Знания.com

Слова с твердым знаком, где после согласного гласная буква дает два звука.

найдите пожалуйста в этом тексте все Средства образной выразительности ,очень надо Добрый вечер тебе!Добрый вечер сегодня всем нам!По домам, по столиц … ам и, нет, деревням и квартирам.Продолжаем свой строить под сердцем единственный храм,Да и что нам ещё остаётся в испуганном мире?Если твой не взрывается мозг от плохих новостей,И с катушек ещё не сошёл. И не пьёшь вечерами,По экрану касаясь своих стариков и друзей…Брось контакты, и я подпишусь на тебя в Instagram’e.Добрый вечер живым, добрый вечер схватившим недуг,Каждый ровня мне, без исключения дня и прописки.Даже если ты вовсе не брат мне и вовсе не друг,Мы под небом одним, мы под Богом одним, в одном списке.Добрый вечер врачам и всем нашим на том рубеже,Что давно отсечён, перекрыт, но пульсирует в такте.Я пишу, нет, кричу со всех сил:Добрый вечер тебе!Напиши мне в ответ, напиши: «У меня всё в порядке».

​​

СРОЧНОО 161Б и Ввот текстНа самую большую планету ,на Юпитер космический корабль не может отпуститься, так как эта планета состоит в основном из газов … . На Венере или на вечерней «звезде», как ее ещё называют, Солнце в течении орбитального года встаёт дважды . На «красной планете» то есть на Марсе в прошлом, возможно, была вода. На планеты гиганты, то есть на газовые шары «ступить нельзя, ведь у них нет Твердой поверхности. На спутнике Земли на Луне происходят землетрясения, то есть лунотресения. На самой ближайшей к Земле планете, на Марсе есть атмосфера​

Допишите промышленные дополнительный дети могли сами улучшаться недавно я прочитала на уроке мы изучали.

Составить текст на Н и НН в причастиях (7 предложений)

Помогите срочно, Сор по русскому. ​

найдите пожалуйста в этом тексте все Средства образной выразительности ,очень надо Добрый вечер тебе!Добрый вечер сегодня всем нам!По домам, по столиц … ам и, нет, деревням и квартирам. Продолжаем свой строить под сердцем единственный храм,Да и что нам ещё остаётся в испуганном мире?Если твой не взрывается мозг от плохих новостей,И с катушек ещё не сошёл. И не пьёшь вечерами,По экрану касаясь своих стариков и друзей…Брось контакты, и я подпишусь на тебя в Instagram’e.Добрый вечер живым, добрый вечер схватившим недуг,Каждый ровня мне, без исключения дня и прописки.Даже если ты вовсе не брат мне и вовсе не друг,Мы под небом одним, мы под Богом одним, в одном списке.Добрый вечер врачам и всем нашим на том рубеже,Что давно отсечён, перекрыт, но пульсирует в такте.Я пишу, нет, кричу со всех сил:Добрый вечер тебе!Напиши мне в ответ, напиши: «У меня всё в порядке».​

Расставь, где это необходимо, запятые. Если поле необходимо оставить пустым, выбери знак «». а) В этом сказании услышим мы: птицы полет В высоте давно … отлетавшей Топот Копыт давно заглохший крики батыров В поединке сразившихся. б) Он крепко держал за повод гончего пса Учара, чтобы тот не вырвался ненароком и не пустился вдогонку за скрывающейся из виду толпой.

в) Притаившийся под обмыском старой промоины крохотный тушканчик выпрыгнул наконец на открытое место. г) В той абсолютной тишине лисица улавливала в воздухе настораживающий её звук витавший над сумеречной степью и никому не принадлежащий. ​

Помогите сделать синтаксический разбор предложения.(Деепричастие).За соблюдение прав граждан гарантируемых конституции обязана следить и государственн … ые органы.​​

родной русский 7 класс заполните таблицу пж 20 с чем то ббаллов​

Как составить сложный план текста

План — это последовательное представление частей содержания текста в кратких формулировках, отражающих тему и (или) основную мысль. Сложный план включает название значительных частей текста, а также их смысловых компонентов. Графическая форма записи сложного плана выглядит следующим образом:

1. …

1.1. …

1.2. …

2. …

2.1. …

2.2. …

2.3. … и т. д.

Алгоритм 1

1. Прочитайте текст и разделите его на смысловые части.

2. Определите основную мысль каждой смысловой части и дайте им названия.

3. Напишите черновик плана, используя для нумерации смысловых частей цифры 1, 2, 3 и т. д.; между названиями смысловых частей оставьте по несколько строк для записи подпунктов.

4. Перечислите для каждой смысловой части составляющие её подпункты, используя для их нумерации цифры 1.1, 1.2, 2.1, 2.2, 2.3 и т. д.

5. Сравните черновик плана с текстом, обращая внимание на следующее:

— всё ли главное нашло отражение в плане;

— связаны ли пункты плана по смыслу;

— отражают ли они основную мысль текста.

6. Проверьте, можно ли, руководствуясь планом, пересказать текст, и, если необходимо, откорректируйте план.

7. Перепишите план на чистовик.

Алгоритм 2

1. Прочитайте текст.

2. Напишите черновик, составляя очень подробный простой план.

3. Преобразуйте простой план в сложный, сгруппировав его компоненты под общими для них заголовками, отражающими основные мысли текста.

4. Сравните черновик плана с текстом, обращая внимание на следующее:

— всё ли главное нашло отражение в плане;

— связаны ли пункты плана по смыслу;

— отражают ли они основную мысль текста.

5. Проверьте, можно ли, руководствуясь планом, пересказать текст, и, если необходимо, откорректируйте план.

6. Пронумеруйте заголовки, отражающие основные смысловые части текста, цифрами 1, 2 и т. д., а соответствующие им подпункты — цифрами 1.1, 1.2, 2.1, 2.2 и т. д.

7. Перепишите план на чистовик.

HISTORIA MAGISTRA VITAE «Информационный»: В помощь ученику

Точка, запятая, двоеточие, точка с запятой, черточка (дефис)	Печатаются без пробела
Перенос, вопросительный и восклицательный знаки	После этих знаков делается пробел
Процент, градус	Пишутся без пробела с цифрой, к кторой они относятся: 115%, 60 о
Кавычки, скобки	Перед раскрытием скобок, кавычек делается пробел, и после закрытия скобок, кавычек делается пробел. Слова, которые заключаются в кавычки, скобки, пишутся без пробела. Журнал «Наука и жизнь»; (аплодисменты)
	Пишется с пробелом до этого знака и после него. Этим тире отличается от черточки (дефиса). Москва – столица нашей родины. 12 – 15%. Но допускается 5-6%, 1993-1994 гг.
Параграф, номер	Отделяются пробелом от цифры, к которой они относятся: № 18; § 23; (§§ 5-6).
Написание некоторых цифр, чисел	4256; 21 245 или 3.245.317; четырехзначные числа разделяют на группы только в таблицах: 6 245 2-я линия; 2-мя сутками; 2-метровый; 3-этажный; 6-ой день. 5 2/3 – целое число отделяется пробелом. Между знаками арифметических действий делается пробел: 100 + 250 = 350; (а + в) = а 2 + 2 ав + в 2
Римские цифры	Для обозначения римских цифр используются заглавные буквы . Римские цифры употребляются для обозначения веков, кварталов года, съездов, конференций, конгрессов, глав учебников и др. В VII главе; ХХ век; VIII съезд.
Некоторые сокращения	См, м, км, км/час, кг, 200 т., 25 кг, 32 см.  После цифры – пробел.

Интеллект-карты: как правильно составить наглядный план для любой задачи

Мы мыслим ассоциациями и образами. Поэтому нам проще запомнить схему, чем несколько страниц текста. Последовательные схемы называют mind maps или интеллект-картами. Рассказываем, как их составить и избежать ошибок

Что такое интеллект-карта

Ментальные карты (интеллект-карты, mind map) — метод организации идей, задач, концепций и любой другой информации. Ментальные карты помогают визуально структурировать, запоминать и объяснять сложные вещи.

Например, записать тезисы выступления или составить учебный план.

В центре всех ментальных карт — главная идея. От нее отходят ключевые мысли, которые можно делить на подпункты до тех пор, пока вы не структурируете всю информацию.

Интеллект-карты придумал британский психолог Тони Бьюзен. В конце 1960-х годов он изучал человеческий мозг и обратил внимание на строение нейронов. Это клетки мозга, которые принимают, обрабатывают и передают информацию другим нейронам. От центра — ядра нейрона отходят отростки, похожие на ветви дерева. Бьюзен организовал информацию по тем же принципам [1]. Согласно исследованию Дэвида Боули из Университета Джонса Хопкинса [2], оценки учащихся, которые пользуются ментальными картами, выше на 12%.

План ремонта квартиры в виде ментальной карты

Для чего нужны интеллект-карты

Ментальные карты помогают в работе, учебе и повседневных задачах. Например, придумывать идеи, запускать проекты, учить языки и планировать отпуск. Вот для чего их чаще всего используют.

Придумывают идеи. В центре карты запишите тему или проблему, а по краям — все идеи, которые придут в голову. В итоге у вас получится визуальная презентация мозгового штурма. Например, темы для блога или концепции нового проекта.

С помощью интеллект-карты можно придумать большую идею бренда или проекта (Фото: MindMeister)

Учатся. С помощью ментальной карты можно разбить компетенцию на несколько навыков и составить учебный план. Например, если вы хотите улучшить навыки текста, нужно научиться писать и редактировать лонгриды, статьи, заметки, посты и работать с другими форматами. Для каждого навыка можно подобрать курс, книгу и лекцию. Если выбираете образовательную программу, запишите в центр нужную компетенцию или профессию, а по краям — подходящие варианты обучения.

С помощью ментальной карты можно разложить компетенцию на умения и навыки

Планируют. Попробуйте спланировать личный бюджет или запустить проект. Например, чтобы организовать мероприятие, нужно поработать над программой, продвижением, технической частью, командой, площадкой. В ментальную карту можно организовать список книг или фильмов. Единственная проблема в том, что к интеллект-картам трудно привязать сроки.

Собирают информацию. В ментальную карту можно уместить книгу, лекцию, статью или вебинар. Разделите лекцию на подтемы и тезисы, а книгу — на главы и основные мысли. Например, подготовить графический конспект доклада для своего выступления. Такой конспект проще запомнить, чем несколько страниц текста.

Попробуйте упаковать выступление Уилла Стивена об идеальном выступлении для TED Talks в интеллект-карту!

Принимают решения. Сначала сформулируйте проблему. Для этого проанализируйте ситуацию и найдите ее причины. Запишите проблему в центр ментальной карты, а по краям — варианты решения. Когда все решения будут перед глазами, выберите наилучшее из альтернатив.

Например, решить, куда вложить свободные деньги: в недвижимость, акции, валюту или образование. Ментальные карты помогут выбрать самый выгодный вариант. Так можно учиться придумывать нестандартные решения и развивать комплекс навыков PSDM — решения проблем и принятия решений.

Способы снять или уменьшить стресс (Фото: AYOA)

Преимущества интеллект-карт

Мы мыслим ассоциациями и образами. Ментальные карты помогают упорядочить информацию и собрать образы в наглядную структуру. При этом изображения вызывают более точные ассоциации, чем буквы. Поэтому мы лучше запоминаем информацию через картинки и иллюстрации [3].

Ментальные карты экономят время восприятия — схему мы считываем быстрее, чем таблицу или список. А если ключевые пункты и ветви выделить разными цветами, можно наглядно показать зоны ответственности.

Как составить интеллект-карту

Интеллект-карты можно составлять в программе или на бумаге. Если работаете на бумаге, записывайте слова печатными буквами. Так мозгу будет проще прочитать схему. Вот несколько шагов для того, чтобы грамотно составить интеллект-карту.

• Разместите лист горизонтально, чтобы по краям вытягивались ветви. Так мозгу будет проще их воспринимать.
• Напишите главное слово, которое опишет всю схему, в центре листа. Например, если создаете интеллект-карту о командной работе, главным словом будет команда.
• Выберите цвет, придумайте ключевой блок и нарисуйте ветвь от главного слова. Старайтесь заключать такие блоки в визуальную рамку. Например, в интеллект-карте о командной работе ключевыми блоками будут люди, правила, цели и роли. Это второй уровень карты.
• Запишите следующие по иерархии ключевые блоки. Отдельно раскройте каждый блок. Например, в правила можно записать: правила совещаний, работы с клиентом, мозгового штурма и планерок в Zoom.
• Продолжайте рисовать следующие уровни интеллект-карты. В итоге у вас получится структура. Возвращайтесь и дополняйте карту, если появляются новые ассоциации.
• Сделайте карту удобнее. Добавьте простые иконки или небольшие картинки для ключевых блоков. Нарисуйте стрелки между отдельными словами, подпишите ветви.
• Попробуйте программы для создания ментальных карт. Например, MindMeister, XMind Zen, MindMup, Mind42, LOOPY.

Семь правил интеллект-карт

1. Располагайте лист горизонтально.
2. Всегда начинайте с центра.
3. Рисуйте ветви от центра в стороны.
4. Заключайте каждый ключевой блок в визуальную рамку.
5. Показывайте иерархию и связь разными цветами.
6. Выбирайте сильные слова для ключевых блоков.
7. Пишите печатными буквами, если работаете на бумаге.

---

В Telegram-канале «Списать не получится» мы еще больше рассказываем о трендах в образовании и о том, как учиться в течение всей жизни и делать это с удовольствием. Подписывайтесь!

Составьте Сложный План 7 Класс Сочинение – Telegraph

>>> ПОДРОБНЕЕ ЖМИТЕ ЗДЕСЬ <<<

Составьте Сложный План 7 Класс Сочинение
Образовака ✍ Русский язык 6 класс Словообразование. Орфография. Культура речи
План текста – это последовательный и связный перечень основных мыслей, которые автор в нем высказывает. Он необходим школьнику для того, чтобы понять, о чем говорил автор, а также лучше запомнить все то, что изложено в его произведении. Таким образом, систематизация текстового материала является необходимостью, позволяющей ученику не только улучшить навыки работы с текстом, но и научиться лучше и быстрее понимать написанное, что поможет ему в будущем.
Материал подготовлен совместно с учителем высшей категории
Опыт работы учителем русского языка и литературы — 27 лет.
Чтобы попасть сюда — пройдите тест.
Будь в числе первых на доске почета
Теперь у нас есть группа — вступай и будь в курсе!

Предметы

Алгебра

Уроки

Тесты по алгебре

Задать вопрос

Английский язык

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

Тесты по английскому языку

Задать вопрос

Биология

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по биологии

Задать вопрос

Всемирная история

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по истории

Задать вопрос

География

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по географии

Задать вопрос

Презентации по географии

Геометрия

Уроки

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по геометрии

Задать вопрос

Информатика

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по информатике

Задать вопрос

История России

Уроки

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по истории России

Задать вопрос

Литература

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Биографии

Краткие содержания

Анализ стихотворений

Анализ произведений

Сочинения

Читательский дневник

Библиотека

Самые краткие содержания

Тесты по литературе

Задать вопрос

Математика

Уроки

2 класс

3 класс

4 класс

5 класс

6 класс

Тесты по математике

Задать вопрос

Обществознание

Уроки

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по обществознанию

Задать вопрос

Окружающий мир

Уроки

1 класс

2 класс

3 класс

4 класс

Тесты по окружающему миру

Задать вопрос

Русский язык

Уроки

1 класс

2 класс

3 класс

4 класс

5 класс

6 класс

7 класс

8 класс

9 класс

10 класс

11 класс

Словари и справочники

Словарь ударений
Орфографические трудности
Морфологический разбор слов
Фонетический разбор слов
Корень слова
Проверочное слово
Как выделить запятыми

Тесты по русскому языку

Задать вопрос

Химия

Уроки

8 класс

9 класс

10 класс

11 класс

Тесты по химии

Задать вопрос

Физика

Уроки

7 класс

8 класс

9 класс

10 класс

11 класс

Тесты по физике

Задать вопрос

Чтение

Уроки

1 класс

2 класс

3 класс

4 класс

Тесты по чтению

Задать вопрос

Еще

Помощь с д/з
Все тесты
Онлайн-батл
Презентации
Учителям
Команда
О проекте
Контакты

Чтобы составить грамотный сложный план текста, нужно понимать, каким критериям должен соответствовать результат. И первый из них – это структурированность, то есть план, как и сам текст, должен иметь начало и конец и вообще полностью соответствовать по структуре исходнику.
Второй важный критерий касается грамотной формулировки заголовков и подзаголовков, которые должны выражать законченную мысль. В хорошем сложном плане они не повторяются и не наслаиваются друг на друга.
Третий критерий – это информативность. Он означает, что, взяв в руки составленный план, школьник не должен испытывать затруднений при пересказе по нему текста. При этом он не должен быть чересчур общим – это сильно помешает при воспроизведении.
И последний критерий – это последовательность, то есть все пункты и подпункты следуют в таком плане друг за другом, последовательность повествования и изложения мыслей не нарушается.
Обращая внимание на пример сложного плана текста, составленный действительно грамотно, можно увидеть, что автор работы опирался на абзацы и выделял самые яркие из использованных в этом тексте образов. Это действительно сильно облегчает выполнение работы.
Приступая к составлению плана, нужно прочитать текст целиком и выделить его главную мысль. После этого нужно разделить весь текст на отдельные смысловые части и придумать им соответствующие заглавия, которые и станут основными пунктами плана. После этого каждая большая часть разделяется на более мелкие по основным мыслям, которые высказывает автор. К этим частям придумываются названия, которые становятся подпунктами.
Такие подпункты должны быть в каждом основном пункте плана и их должно быть не меньше двух.
После этого нужно проверить, насколько удачно сформулированы пункты и подпункты: они не должны быть просто цитатами из текста или выдержками из отдельных предложений. Также нужно проверить, насколько хорошо этот план отражает структуру текста и его основную мысль.
В качестве примера можно рассмотреть план текста о феодальной раздробленности Руси, который легко найти в учебнике истории.
1.Феодальная раздробленность: причины явления.
а) социально-экономические предпосылки; б) политические предпосылки.
2. Как развивалась Русь в период феодальной раздробленности.
а) русские княжества и специфика их развития; б) культура этого исторического периода; в) борьба с иноземными захватчиками.
3. Последствия феодальной раздробленности.
а) социально-экономические последствия; б) политические последствия.
По составленному таким образом плану школьник без труда может воспроизвести главу из учебника, так что полученный навык можно и нужно использовать при подготовке к экзаменам.
Составление сложного плана – это полезный навык. Он делается по определенной схеме и должен соответствовать четырем критериям. По хорошо составленному сложному плану школьник с легкостью может воспроизвести исходный текст.
Средняя оценка: 4.6 . Всего получено оценок: 306.
Не понравилось? — Напиши в комментариях, чего не хватает.

Полное или частичное копирование материалов разрешается только с указанием активной гиперссылки на https://obrazovaka. ru
Copyright © 2008-2020 Образовака Пользовательское соглашение
Политика конфиденциальности
Контакты

5. Составьте сложный планПомогите пожалуйста соч по русскому 7 класс !!!!
Сложный план текста – пример | Как составить сложный план : порядок работы
План сочинения : как составить , пример
Урок по теме «Простой и сложный план текста» в 7 классе
Составляем план сочинения | Сайт учителя русского языка и литературы
Памятка «Как составить тезисный план » | Методическая…
План текста-рассуждения / Памятки / Справочник по русскому языку 5-9 класс
Как составить план сочинения по литературе? Инструкция с примером
План текста — простой, сложный , тезисный — YouTube
Составить сложный план на тему : сочинение за природу в ответе каждый
Составляем план сочинения
План сочинения | СЛОЖНЫЙ ПЛАН
Как составлять план текста: супер-шпаргалка по русскому
Что такое план статьи и как его правильно составить : советы и примеры
Как составить план текста по русскому языку
Реферат На Тему Политические Партии
Папка Для Курсовой Работы Как Называется
Сочинение Про Мусы Джалиля На Татарском Языке
Список Литературы Для Написания Декабрьского Сочинения
Правоохранительные Органы Рф Курсовая

А тугомент у тебя есть? Обучение работе с историческими документами

Систематизация основных умений и навыков работы с историческими документами (ИД) на основе документально-методических комплексов (ДМК) включает в себя обязательный минимальный уровень знаний и умений для учащихся 5-6-х и 7-8-х классов и желаемый уровень для выпускника основной школы (9-й класс).

– это обобщающая схема анализа исторического документа. При работе с документами важно заинтересовать ребят, создать ситуацию, стимулирующую интерес и творческую активность. Здесь выручит игра. Например, на уроке по теме «Нашествие Батыя» ученикам предлагается несколько документов в виде рукописей в свитках, с обгоревшими краями. Дети играют роль исследователей, отправившихся на машине времени в прошлое. Перед ними стоят задачи: восстановить ход событий, составить словарик исторических терминов, сделать все возможные выводы. Вывод по уроку делается или устно или после заполнения карты исследования в письменном виде. обязательно сдается на проверку учителю. Часто на одном из последних уроков какой-либо темы мы проводим лабораторно-практическое занятие – составляем сборник документов по теме. Алгоритм работы следующий:

Умения и навыки

Система может корректироваться (усложняться или упрощаться) по желанию учителя, взявшего ее на вооружение. Главное, чтобы были соблюдены базовые принципы преемственности, системности и развития. Например, если выпускник 5-го класса должен уметь составить простой рассказ о событиях (о личности) с использованием ИД, то выпускник 6-го – развернутый рассказ с использованием нескольких ИД. Далее если будет соблюден принцип преемственности и работа над формированием основных умений и навыков будет проходить в системе, то выпускник 7-го класса сможет анализировать ИД в контексте исторической ситуации, а также уметь использовать ИД для доказательства собственного мнения. Восьмиклассник уже вполне способен проводить поиск необходимой информации и уметь выстраивать собственные суждения, опираясь на материал одного или нескольких ИД. Характерные умения и навыки для выпускника основной школы собраны под грифом «желаемый уровень». Развить умения, названные ниже под номерами 9.3, 9.4, 9.5, 9.6, возможно лишь при соблюдении преемственности и работы в системе на всех этапах обучения.

Ниже приведен обязательный минимум для учащихся 5-6-х классов. Задача – извлечение сведений простого характера из ИД.

5.1. Уметь определить тип документа.

5.2. Уметь определить время написания ИД или историческую эпоху.

5.3. Уметь определить автора (если возможно) или принадлежность предполагаемого автора к социальной группе.

5.4. Уметь расположить несколько ИД в хронологическом порядке.

5.5. Уметь работать с ИД по отдельным вопросам учителя.

5.6. Уметь составить конкретные вопросы к документу.

5.7. Уметь пересказать содержание ИД.

5.8. Уметь составить простой рассказ о событиях (о личности) с использованием ИД.

6.1. Уметь анализировать ИД по предлагаемому плану.

6.2. Уметь составить развернутый рассказ с использованием нескольких ИД.

Обязательный минимум для учащихся 7-8-х классов подразумевает более глубокий аналитический характер работы.

7.1. Уметь составить вопросы к ИД более глубокого аналитического характера.

7.2. Уметь анализировать ИД по предлагаемому плану (более сложный план).

7.3. Уметь анализировать ИД в контексте исторической ситуации.

7.4. Уметь использовать ИД для доказательства какого-либо исторического факта, события, собственного мнения.

8.1. Уметь проводить поиск необходимой информации в одном или нескольких ИД.

8.2. Уметь выстраивать собственные суждения, опираясь на материал одного или нескольких ИД.

Желаемый уровень для выпускника основной школы (9-й класс) предусматривает творческий характер работы с ИД.

9.1. Уметь отбирать необходимый материал из нескольких ИД для самостоятельного решения учебной задачи.

9.2. Уметь сопоставлять ИД с другими историческими источниками.

9.3. Уметь сопоставлять ИД, отражающие различные взгляды на одно и то же событие.

9.4. Уметь выявлять причинно-следственные связи событий и фактов, отраженных в ИД.

9.5. Уметь извлекать из нескольких ИД необходимую информацию, обобщать и анализировать ее.

9.6. Уметь свободно оперировать информацией, добытой в результате анализа нескольких ИД.

Этапы работы с историческими документами

Обучение работе с ИД я организую по следующим направлениям:

1. Обучение постановке вопросов к ИД.

2. Обучение составлению плана исследования.

3. Формирование умения анализировать содержание исторического документа.

Обучение постановке вопросов к ИД предполагает 4 этапа: изучение содержания текста и обсуждение в группах, социализация, ранжирование, обобщение.

Обучение составлению плана исследования предполагает использование памяток, составление памяток, формирование умения трансформировать вопросы в повествовательные предложения.

Формирование умения анализировать содержание ИД предполагает 7 позиций – от определения типа документа до установления информативных возможностей содержания документа для решения обозначенной проблемы.

Для работы с ИД основополагающим является умение поставить вопросы к конкретному ИД (это умение для 5-6-х классов). Для его формирования автор применяет описываемую ниже методику.

1-й этап. Ребятам предлагается составить все возможные вопросы к конкретному ИД (работа проходит индивидуально, в парах или в группах).

2-й этап. Один из учащихся озвучивает вопросы, а класс сравнивает их со своими, отсеивая похожие или аналогичные (часто схожие вопросы объединяются и записываются в более точной формулировке).

3-й этап. Учащиеся коллективно под контролем учителя выстраивают вопросы в логической последовательности.

4-й этап. Один из учащихся анализирует документ в соответствии с получившимся планом.

Пример плана анализа, составленного учащимися 5-го класса, к документу «Из законов царя Хаммурапи»:

1. К какому типу относится документ?

2. В какое время могли быть написаны законы?

3. Кто автор законов? Мог ли их написать кто-то другой?

4. Определить, на какие категории делилось население Древнего Вавилона.

5. Было ли неравенство среди людей? Считалось ли оно справедливым?

6. Можно ли определить основные занятия жителей Древнего Вавилона?

7. Зачем Хаммурапи ссылается на Бога Солнца?

8. Можно ли применять эти законы сегодня?

Важно, чтобы ученики уяснили, что бывают разные аналитические вопросы. Для этого применяется следующий прием: ребятам предлагается дома составить вопросы к документу так, чтобы набрать 10 баллов.

Условие: вопросы, начинающиеся со слов «кто», «что» «когда», оцениваются в 1 балл, а вопросы, начинающиеся со слов «зачем», «почему», «с какой целью», – в 2 балла. Ребята учатся обращать внимание на любые мелочи в тексте, которые могут оказаться очень важными в дальнейшем.

Постановка вопросов помогает более глубоко осмыслить содержание документа и, главное, увидеть внутренние причинно-следственные связи источника, проследить логику авторского изложения материала.

В конечном итоге у ребят формируется умение структурировать текст и отбирать полезную информацию.

Обучение составлению плана исследования проблемы

Ученик чувствует себя комфортно на уроке, когда четко понимает, что он будет делать (видна конкретная цель, ясен путь). Неудачи поджидают его, если логика изучения тем не меняется на всем протяжении школьного курса истории. Это такие темы, как характеристика войны, конкретной битвы, исторической личности, восстания, экспедиции, реформ и т. д.

В этой работе учащихся выручают памятки, взятые из методической литературы. Их можно разложить на партах и пользоваться с самого начала урока. Следующий шаг в обучении составлению плана – совместное создание плана исследования. Для этого определяется перечень вопросов, они ранжируются согласно логике изучения проблемы. После того как вырисовывался конкретный план изучения темы, предлагается для сравнения план изучения подобной темы, составленный учителем или взятый из какого-либо источника.

Например, на уроке «Иван Грозный: личность и время» ученики 7-го класса составили следующий план исследования:

1. Когда родился Иван IV? Кто были его родители?

2. Как проходило его детство?

3. Происхождение и положение Ивана IV.

4. Каковы черты характера? Что повлияло на его формирование?

5. Каковы цели его царствования?

6. Каковы итоги его царствования?

7. Как он повлиял на развитие страны?

8. Мое отношение к Ивану IV Грозному.

Для сравнения учащимся был предложен вариант памятки оценки исторической личности из книги Н.И. Запорожца «Формирование классового подхода к оценке исторических деятелей»:

1. Определить условия, в которых формировался характер личности.

2. Раскрыть черты характера, определить, какие качества личности помогли ему в достижении целей и задач, стоящих перед народом и страной.

3. Выразить свое отношение к личности.

4. Оценить роль личности в истории страны, ее влияние на последующий ход событий.

Детям задается вопрос: «Чем отличается ваш план от предложенного учителем?». Внимание заостряется на том, что план может быть не только в форме вопросов, но и в виде повествовательных утверждений, задающих алгоритм исследовательской работы.

Важно довести до автоматизма умение ребят выдвигать пункты плана исследования какого-либо исторического события, какой-либо проблемы, личности и т.д. Это сократит время для анализа документов, а в дальнейшем позволит более уверенно браться за написание реферата, доклада и т. п..

Формирование умения анализа содержания исторического документа

Анализ содержания ИД предполагает:

1. Определение типа документа.

2. Установление автора.

3. Уточнение даты создания документа.

4. Выяснение сути документа.

5. Прогнозирование цели создания документа.

6. Выявление информации, относящейся к обозначенной проблеме.

Установление информационных возможностей содержания документа для решения проблемы.

Обучение анализу содержания исторического документа осуществляется в несколько этапов. Первоначальную информацию о типологии исторических документов ребята получают от учителя, а затем вместе (можно в игровой или состязательной форме) определяют 1-2 существенных признака каждого типа документа. Приведу примеры.

а) Летописи – хронологическое описание событий. Начинались со слов «В лето…» (повествование велось по годам).

б) Мемуары – воспоминания участников событий (субъективность прочтения).

в) Грамоты – подтверждение чьих-либо прав (льгот), деловые документы.

г) Жития – жизнеописание исторических лиц, причисленных к лику святых.

д) Былины – народные песни-сказания (воспевание подвигов богатырей).

Не менее важно при анализе любого документа формирование умений отвечать на следующие вопросы: Кто автор? Когда был создан документ? Какие исторические факты, события в нем описываются? В чем основная идея? С какой целью был создан документ? Обогатил ли документ ваши знания по проблеме? Дает ли документ возможность изучить проблему?

Следующий этап – составление плана анализа документа в 5-6-х классах. План анализа документа предлагается учителем. Я применяю авторский вариант:

«Знакомство с содержанием (название, автор, дата, суть…).

Что это за исторический документ? (Письмо, воспоминание, текст песни, дневник, цитата). Это точка зрения непосредственного участника событий или взгляд второстепенного лица? Каков исторический фон? Какие следуют выводы? Можно ли доверять документу? Каково ваше отношение к полученным фактам?»

Это позволяет ребятам в 9-м классе при анализе ДМК автоматически классифицировать предлагаемые документы и отбирать необходимую информацию. Для учащихся 9-го класса я предлагаю более сложный план анализа документов (Ерохина М.С., Короткова М.В. Уроки Клио. – М.: МИРОС, 2000), входящих в ДМК:

«Какой тип ИД? С какой целью написан? Какой проблеме посвящен? Какую информацию содержит? Как отражает взгляды автора? Есть ли предубеждения, стремление навязать свою точку зрения? Какие мысли автора вызывают сомнения? Какие противоречат другим свидетельствам? Дайте общую оценку качества документа».

Анализ содержания исторического документа зависит от типа документа и завершается обобщающими выводами (в виде таблицы, схемы, утверждения).

Варианты анализа в зависимости от типа документа

Каждый ИД обладает свойствами, которые присущи только ему, их надо уловить. Именно это определяет характер и глубину работы с ИД, а также способ анализа.

а) При анализе государственных законов применяются следующие вопросы: «Когда, где и почему появился закон (сборник законов)? Кто автор законов? Чьи интересы защищает закон? Охарактеризуйте основные положения закона (ссылки на текст, цитирование). Сравните с предыдущими законами. Что изменилось после введения закона? Ваше отношение к этому законодательному акту (справедливость, необходимость и т.д.)».

б) При анализе летописных источников используются следующие вопросы: «О каких событиях идет речь в документе? Как автор излагает ход событий, определяет их значение, объясняет причины? Какова позиция автора? Совпадает ли с современной точкой зрения?»

в) Вопросы к анализу свидетельств очевидцев (письма, мемуары): «Кто автор? О каких событиях идет повествование? Автор является участником событий, свидетелем или судит с чьих-то слов? Какова позиция автора? Чем это объяснить? Можно ли доверять автору? Почему? Как мнение автора соотносится с другими источниками по проблеме? А с вашим мнением?»

Ученики должны четко ответить на вопросы о том, есть ли в ИД материал, позволяющий использовать его для раскрытия проблемы, как его можно использовать и какие выводы можно сделать?

Карта исследователя

Карта исследователя – это обобщающая схема анализа исторического документа. При работе с документами важно заинтересовать ребят, создать ситуацию, стимулирующую интерес и творческую активность. Здесь выручит игра. Например, на уроке по теме «Нашествие Батыя» ученикам предлагается несколько документов в виде рукописей в свитках, с обгоревшими краями. Дети играют роль исследователей, отправившихся на машине времени в прошлое. Перед ними стоят задачи: восстановить ход событий, составить словарик исторических терминов, сделать все возможные выводы.

В ходе урока они заполняют карту исследователя. (См. таблицу 1).

Подобные карты заполняются и на других уроках-исследованиях (по типу это лабораторно-практические занятия). Например, в 9-м классе на уроке по теме «Тоталитаризм: признаки и проявления его в СССР» ученики, работая с ДМК, заполняют следующую карту исследователя. (См. таблицу 2).

Вывод по уроку делается или устно или после заполнения карты исследования в письменном виде. Карта исследователя обязательно сдается на проверку учителю. Часто на одном из последних уроков какой-либо темы мы проводим лабораторно-практическое занятие – составляем сборник документов по теме. Алгоритм работы следующий:

1. Ребята изучают предложенный им ДМК (групповая работа).

2. Определяют и формулируют тему (это название сборника).

3. Отбирают документы по определенной логике (критерии учащиеся определяют сами).

4. Защищают проект.

Формы внеклассной работы

Внеклассная работа в основном проводится летом, при школьном краеведческом лагере дневного пребывания. Задача – поиск и накопление краеведческого материала, анализ и осмысление которого происходит во время учебного года. Во время лагерной смены дети должны активно и интересно отдыхать, поэтому я пытаюсь обычную поисковую работу облачить в нестандартные, игровые формы.

День Шерлока Холмса. Алгоритм игры: ребята делятся на группы, каждая из которых получает план села Кубенское, относящийся к концу XIX века; задание – реконструировать конкретный район села, сравнить полученную картину с реальной, сделать все возможные выводы.

Читаем краеведов (используется в пасмурные дни).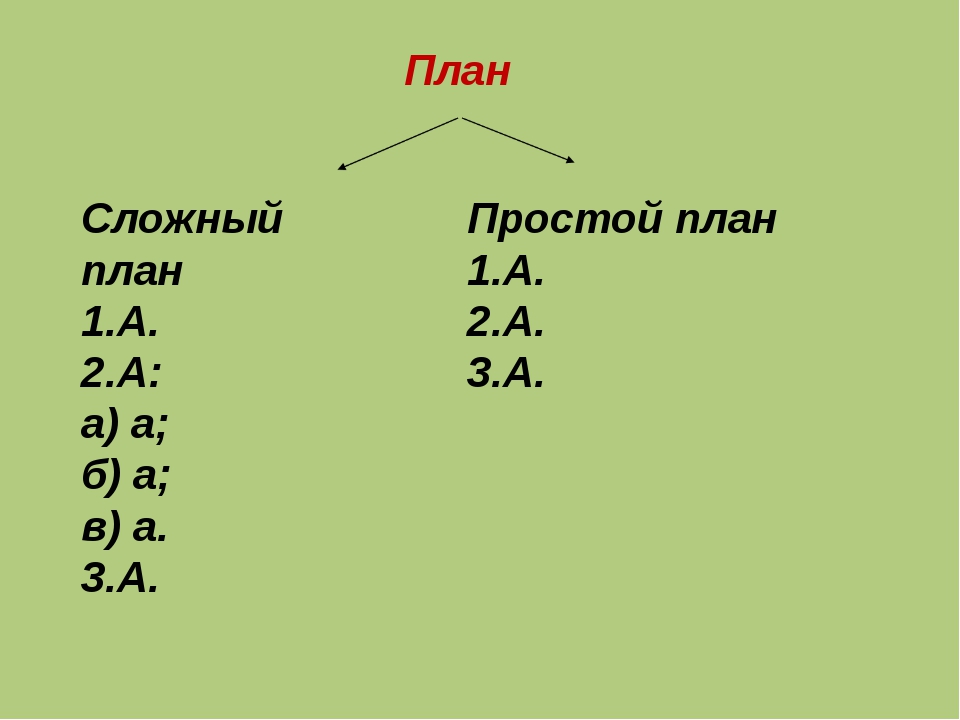 Алгоритм игры: ребята делятся на группы, каждая из которых получает текст (это может быть любой краеведческий материал) и задание – подготовить рассказ, начинающийся со слов «А вы знаете, что…». Группы оформляют изученный материал в виде странички «Книги для чтения по истории села Кубенское», который затем можно использовать на уроках и классных часах.

Остановись, мгновение (фоторепортаж о сохранившихся памятниках деревянной архитектуры села). Алгоритм игры: ребята получают маршрутные карты с заданием запечатлеть то, что, по их мнению, представляет интерес или скоро может исчезнуть (село ветшает, на месте старых построек возникают новые, деревянные дома горят и т.д.). Оформляется фотоматериал в виде альбома или вывешивается на стенд с обязательными комментариями по истории дома.

Идем путем Ивана Грозного (дневной поход).

Через наше село, находящееся на старом Кирилловском тракте (Вологда – Кириллов) несколько раз проезжал Иван Грозный, следуя в Кирилло-Белозерский монастырь. Мы готовимся к походу по методике КМД с обязательным предварительным изучением эпохи и созданием ролевой игры.

В системе внеурочной деятельности предусмотрены также выполнение заданий краеведческого музея, встречи с ветеранами, местными художниками и поэтами, запись воспоминаний пожилых людей и т.д. Все это находит отражение в творческих отчетах о проделанной работе за смену. Параллельно идет накопление дидактического материала для кабинета истории и изучается местная документальная база.

Сложный самолет

	Нет, , а не , эта комплексная плоскость …
… это комплексная плоскость:	A самолет для комплексных номеров !

(Также называется «диаграммой Аргана»)

Реальное и воображаемое составляют комплекс

Комплексное число — это комбинация действительного и мнимого числа:

Реальный номер — это тип номера, который мы используем каждый день.

Примеры: 12,38, ½, 0, −2000

Когда мы возводим в квадрат действительное число, мы получаем положительный (или нулевой) результат:

2 ² = 2 × 2 = 4
1 ² = 1 × 1 = 1
0 ² = 0 × 0 = 0

Что мы можем возвести в квадрат, чтобы получить −1?

? ² = -1

Возведение в квадрат −1 не работает, потому что умножение отрицательных чисел дает положительное значение: (−1) × (−1) = +1, и никакое другое действительное число также не работает.

Значит математика кажется неполной …

… но мы можем заполнить пробел на , представив , есть число, которое при умножении на само себя дает −1
(назовем его i для мнимого):

я ² = -1

И вместе:

Комплексное число — это комбинация действительного и мнимого числа

Примеры: 3,6 + 4 i , −0,02 + 1,2 i , 25-0.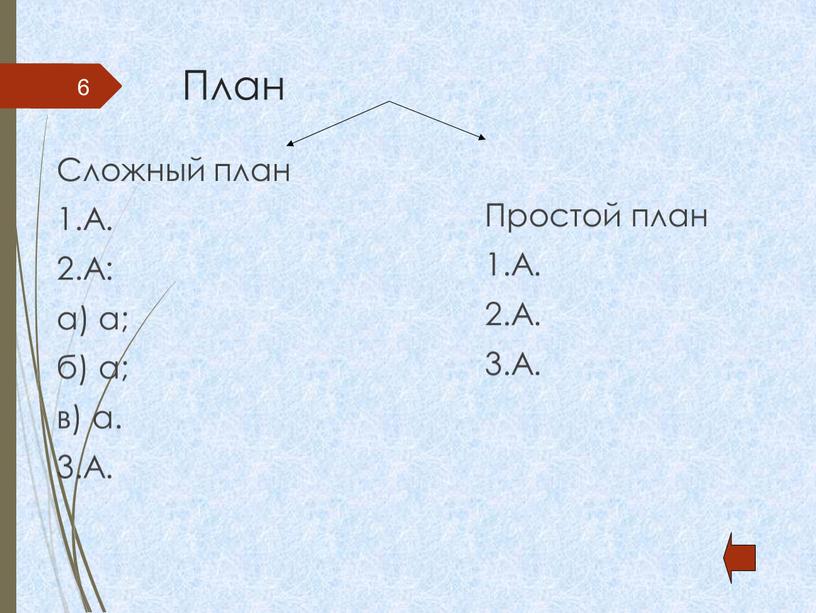 3 i , 0 + 2 i

Отображение комплексного числа на плоскости

Возможно, вам знакома числовая строка:

Но где мы помещаем комплексное число вроде 3 + 4 i ?

Пусть линия вещественных чисел идет влево-вправо, как обычно, а линия мнимых чисел идет вверх и вниз :

Затем мы можем построить комплексное число, например 3 + 4i : 3 единицы по (действительная ось), и 4 единицы вверх (мнимая ось).
А вот 4 — 2i : 4 единицы по (действительная ось), и на 2 единицы вниз (мнимая ось).

А это комплексная плоскость :

• комплексный , потому что это комбинация действительного и мнимого,
• плоскость потому что она похожа на геометрическую плоскость (2-х мерную).

Весь новый мир

Теперь давайте перенесем идею о плоскости (декартовы координаты, полярные координаты, векторы и т. Д.) В комплексные числа.

Он откроет совершенно новый мир чисел, более полных и элегантных, как вы увидите.

Комплексное число как вектор

Мы можем думать о комплексном числе как о векторе.

Это вектор.
Имеет величину (длину) и направление.

А вот и комплексное число 3 + 4i как вектор :

Добавление

Вы также можете складывать комплексные числа как векторы:

Чтобы сложить комплексные числа 3 + 5i и 4 — 3i : сложите действительные числа и сложите мнимые числа отдельно, вот так: (3 + 5 i ) + (4 — 3 i ) = (3 + 4) + (5 — 3) i = 7 + 2 и

Полярная форма

Давайте снова воспользуемся 3 + 4i :
Вот в полярной форме:

Таким образом, комплексное число 3 + 4i также может отображаться как расстояние (5) и угол (0. 927 радиан).

Давайте посмотрим, как преобразовать из одной формы в другую, используя преобразование из декартовой системы координат в полярную:

Пример: номер

3 + 4i

из 3 + 4i :

• r = √ (x ² + y ² ) = √ (3 ² + 4 ² ) = √25 = 5
• θ = tan ^-1 (y / x) = tan ^-1 (4/3) = 0,927 (до 3 знаков после запятой)

И получаем расстояние (5) и угол (0.927 радиан)

Снова:

• x = r × cos ( θ ) = 5 × cos (0,927) = 5 × 0,6002 … = 3 (достаточно близко)
• y = r × sin ( θ ) = 5 × sin (0,927) = 5 × 0,7998 … = 4 (достаточно близко)

И расстояние 5 и угол 0,927 снова становятся 3 и 4

На самом деле, обычный способ записать комплексное число в полярной форме — это

.

x + i y = r cos θ + i r sin θ

= r (cos θ + i sin θ )

И «cos θ + i sin θ » часто сокращается до «cis θ », поэтому:

x + iy = r цис θ

cis — это просто сокращение для cos θ + i sin θ

Итак, мы можем написать:

3 + 4i = 5 цис 0. 927

В некоторых предметах, например, в электронике, «цис» используется очень много!

Сводка

• Комплексная плоскость — это плоскость, на которой:
  • вещественные числа слева направо и
  • мнимых числа, бегущих вверх-вниз.
• Чтобы преобразовать из декартовой в полярную форму:
  • r = √ (x ² + y ² )
  • θ = tan ^-1 (y / x)
• Чтобы преобразовать полярную форму в декартову:
  • x = r × cos ( θ )
  • y = r × sin ( θ )
• Полярная форма r cos θ + i r sin θ часто сокращается до r cis θ

Далее… узнать об умножении комплексных чисел.

комплексная плоскость, сложение и вычитание

Комплексные числа: комплексная плоскость, сложение и вычитание Поскольку Гаусс доказал фундаментальную теорему алгебры, мы знаем, что все комплексные числа имеют форму x + yi, , где x и y — действительные числа, действительные числа, — все числа, которые являются положительными. , отрицательное или нулевое.Следовательно, мы можем использовать плоскость xy для отображения комплексных чисел. Мы даже назовем это комплексной плоскостью , когда будем использовать таким образом плоскость xy . Это дает нам второй путь к комплексным числам, первый из которых алгебраически, как в выражении x + yi.

Обозначение.

Стандартный символ для набора всех комплексных чисел — C , и мы также будем называть комплексную плоскость C .

Мы попробуем использовать x и y для вещественных переменных и z и w для комплексных переменных. Например, уравнение z = x + yi следует понимать как говорящее, что комплексное число z является суммой действительного числа x и действительного числа y , умноженного на i. В общем, часть x комплексного числа z = x + yi называется действительной частью z , а y называется мнимой частью z . (Иногда yi называют мнимой частью.)

Когда мы используем плоскость xy для комплексной плоскости C , мы будем называть ось x именем действительной оси , и ось y мы назовем мнимая ось.

Вещественные числа следует рассматривать как частный случай комплексных чисел; это просто числа x + yi , когда y равно 0, то есть это числа на действительной оси.Например, действительное число 2 — это 2 + 0 i. Числа на мнимой оси иногда называют чисто мнимыми числами.

Арифметические операции на

C Операции сложения и вычитания легко понять. Чтобы сложить или вычесть два комплексных числа, просто сложите или вычтите соответствующие действительные и мнимые части. Например, сумма 5 + 3 i и 4 + 2 i составляет 9 + 5 i. Для другого сумма 3 + i и –1 + 2 i составляет 2 + 3 i.

Сложение может быть представлено графически на комплексной плоскости C . Возьмем последний пример. Комплексное число z = 3 + i расположено на 3 единицы справа от мнимой оси и на 1 единицу выше действительной оси, а w = –1 + 2 i расположено на 1 единицу слева и 2 единиц вверх. Таким образом, сумма z + w = 2 + 3 i равна 2 единицам вправо и на 3 единицы больше.

Правило параллелограмма.

Обратите внимание, что в последнем примере четыре комплексных числа 0, z = 3 + i, w = –1 + 2 i, и z + w = 2 + 3 i равны углы параллелограмма. В целом это правда. Чтобы найти, где на плоскости C расположена сумма z + w двух комплексных чисел z и w , на графике z и w, проведите линии от 0 до каждого из них, и завершаем параллелограмм.Четвертая вершина будет иметь вид z + w.

Дополнение как перевод.

Используя правило параллелограмма, можно интерпретировать сложение по w как преобразование плоскости C . Добавление w к 0 дает w, конечно, , поэтому 0 перемещается в w в этом преобразовании. Любая другая точка z перемещается в z + w, , поэтому z перемещается в том же направлении на такое же расстояние.Другими словами, каждая точка в C перемещается в том же направлении и на то же расстояние, когда к нему добавляется w . Можно сказать, что сложение w дает перевод плоскости C в направлении и на расстояние от 0 до w. Термин «вектор» обычно используется в описании: «плоскость смещена по вектору 0 w.

Отрицание и вычитание.

Есть и красивая геометрическая интерпретация отрицания.Конечно, отрицание x + yi составляет — x — yi, , поэтому отрицание комплексного числа будет расположено прямо напротив 0 и на таком же расстоянии. Например, z = 2 + i располагается на 2 единицы вправо и на одну единицу вверх, поэтому его отрицание — z = –2 — i располагается на 2 единицы слева и на одну единицу ниже.

Отрицание можно интерпретировать как преобразование плоскости C тоже. Если повернуть плоскость на 180 ° вокруг 0, то каждая точка z отправляется в свое отрицание — z. Таким образом, отрицание дает поворот на 180 °.

Используя сложение и отрицание, вы можете определить геометрическое правило вычитания. Чтобы найти, где будет z — w , сначала инвертируйте w , найдя точку напротив 0, а затем используйте правило параллелограмма.

Мы можем интерпретировать вычитание w как преобразование C : плоскость перемещается по вектору от 0 до — w. Другими словами, плоскость перемещается по вектору w 0.

Полярная форма комплексного числа

Полярная форма комплексное число — еще один способ представления комплексного числа. Форма z знак равно а + б я называется прямоугольной координатной формой комплексного числа.

Горизонтальная ось — действительная ось, а вертикальная ось — мнимая ось. Мы находим реальные и сложные компоненты с точки зрения р и θ где р — длина вектора и θ — угол с действительной осью.

От Теорема Пифагора :

р 2 знак равно а 2 + б 2

Используя базовый тригонометрические соотношения :

потому что θ знак равно а р и грех θ знак равно б р .

Умножая каждую сторону на р :

р потому что θ знак равно а и р грех θ знак равно б

Прямоугольная форма комплексного числа задается формулой

z знак равно а + б я .

Подставьте значения а и б .

z знак равно а + б я знак равно р потому что θ + ( р грех θ ) я знак равно р ( потому что θ + я грех θ )

В случае комплексного числа р представляет абсолютная величина или модуль и угол θ называется аргументом комплексного числа.

Это можно резюмировать следующим образом:

Полярная форма комплексного числа z знак равно а + б я является z знак равно р ( потому что θ + я грех θ ) , где р знак равно | z | знак равно а 2 + б 2 , а знак равно р потому что θ и б знак равно р грех θ , и θ знак равно загар — 1 ( б а ) за а > 0 и θ знак равно загар — 1 ( б а ) + π или θ знак равно загар — 1 ( б а ) + 180 ° за а < 0 .

Пример:

Выразите комплексное число в полярной форме.

5 + 2 я

Полярная форма комплексного числа z знак равно а + б я является z знак равно р ( потому что θ + я грех θ ) .

Итак, сначала найдите абсолютное значение р .

р знак равно | z | знак равно а 2 + б 2 знак равно 5 2 + 2 2 знак равно 25 + 4 знак равно 29 ≈ 5. 39

Теперь найдите аргумент θ .

С а > 0 воспользуйтесь формулой θ знак равно загар — 1 ( б а ) .

θ знак равно загар — 1 ( 2 5 ) ≈ 0.38

Обратите внимание, что здесь θ измеряется в радианах.

Следовательно, полярная форма 5 + 2 я около 5,39 ( потому что ( 0,38 ) + я грех ( 0,38 ) ) .

Как складывать комплексные числа в комплексной плоскости — видео и стенограмма урока

Как их сложить

С этой векторной формой и нашей комплексной плоскостью теперь мы можем очень легко складывать наши комплексные числа вместе.Все, что нам нужно сделать, это переместить один из наших векторов так, чтобы он начинался там, где заканчивается другой. Переместим синюю стрелку так, чтобы она начиналась там, где заканчивается красная стрелка.

Когда мы это сделали, наш ответ — точка, на которую указывает синяя стрелка. Это (13, 2). Это дает нам комплексное число 13 + 2 i .

Мы также могли переместить красную стрелку так, чтобы она начиналась там, где заканчивается синяя стрелка. Когда мы это сделаем, красная стрелка укажет на наш ответ.

Рассмотрим еще парочку примеров.

Пример 1

Складываем -6 + 10 i и 4 + 2 i .

Сначала мы наносим точки (-6, 10) и (4, 2) на нашу комплексную плоскость. Затем рисуем стрелки из начала координат.

Затем перемещаем одну из стрелок так, чтобы она начиналась там, где заканчивается другая.

Мы видим, что он указывает на (-2, 12).Итак, наш ответ — -2 + 12 i .

Пример 2

Складываем 1 + 3 i и 4 + 5 i

Здесь мы сделаем то же самое. Сначала мы наносим точки (1, 3) и (4, 5). Затем мы рисуем стрелки к каждому.

Затем перемещаем одну из стрелок так, чтобы ее начало соединилось с концом другой стрелки.

Мы видим синюю стрелку, указывающую на точку (5, 8).Это говорит нам, что ответ — 5 + 8 i .

Резюме урока

Давайте рассмотрим то, что мы узнали. Комплексное число — это число, имеющее как действительную, так и мнимую части. i означает мнимое и представляет собой квадратный корень из -1.

Чтобы сложить комплексные числа на комплексной плоскости, сначала наносим точки. Комплексное число — a + bi и строится в точке ( a , b ).Реальная часть сообщает нам, где она будет на действительной оси, а мнимая часть сообщает нам, где находится точка на мнимой оси. Комплексная плоскость аналогична декартовой плоскости, за исключением того, что у нее есть действительная ось для оси x и мнимая ось для оси y. Затем мы рисуем стрелки к каждому из начала координат, создавая их векторные формы. Затем, чтобы найти ответ, мы перемещаем одну стрелку так, чтобы ее начало находилось в конце другой стрелки. Где указывает наша стрелка, и есть наш ответ.

Краткий урок

Сложение комплексных чисел выполняется на комплексной плоскости, которая похожа на декартову плоскость. Комплексное число — это число, имеющее как действительную, так и мнимую части.

Стрелки, начинающиеся с начала координат, указывают на векторную форму комплексного числа.

Результаты обучения

Примените свое понимание процесса сложения комплексных чисел, выполнив следующие действия:

• Прочтите определение математического термина «комплексное число»
• Сравните сложную плоскость с декартовой плоскостью
• Сложить комплексные числа в данном уравнении

Объяснение

комплексных чисел.Когда мы думаем о комплексных числах, мы… | Бретт Берри | Math Hacks

Когда мы думаем о комплексных числах, мы часто думаем о выполнении алгебры с этим странным термином i , и все это кажется немного произвольным и легко забываемым. На самом деле то, что мы делаем, осязаемо и может быть визуализировано.

Итак, готовьтесь.

После этого поста вы, вероятно, никогда больше не будете думать о комплексных числах по-прежнему… и да, это хорошо.

Примечание: Если вы не знаете, что такое мнимые числа и как они действуют на комплексной плоскости, посмотрите этот пост .

Комплексные числа — это сумма действительного и мнимого числа, представленная как a + b i. Используя комплексную плоскость, мы можем построить комплексные числа аналогично тому, как мы наносим координаты на декартову плоскость.

Вот несколько примеров:

3 + 2 i

1 — 4 i

-3 + 3,5 i

Просто нарисуйте точку на пересечении действительной части, найденную на горизонтальная ось и мнимая часть, расположенная на вертикальной оси.

Это, безусловно, самая простая и интуитивно понятная операция. Сложение / вычитание действительных чисел переводит точку вправо / влево на действительной оси, а добавление / вычитание мнимых чисел переводит точку вверх / вниз на мнимой оси.

Арифметически это работает так же, как объединение одинаковых терминов в алгебре.

Например, если мы вычтем 1-4 i из 3 + 2 i, , мы просто вычислим действительную разницу:

3-1 = 2,

и мнимую разницу:

2 i — (-4 i ) = 2 i + 4 i = 6 i.

Это то же самое, что построить точку 3 + 2 i и перенести ее на влево на 1 единицу и на 4 единицы на . В результате получается ответ: 2 + 6 i.

Мы также можем рассматривать эти точки как векторов .

Сначала разложите знак минус, чтобы получилось сложение: (3 + 2 i ) + (-1 + 4 i ).

Затем постройте две точки с отрезками прямой, выходящими из исходной точки.

Чтобы сложить эти точки, просто наложите одну на другую. Поскольку сложение коммутативно, не имеет значения, каким образом мы их складываем.

Это может показаться излишним, но вот что: понимание векторного представления значительно упростит умножение и деление комплексных чисел.

Эта операция немного менее очевидна и заставляет задуматься:

Что означает умножение двух комплексных чисел вместе?

В общем, мы знаем, что умножение на действительное число масштабирует значение, и мы узнали в последнем посте, что умножение на i поворачивает значение на 90˚ против часовой стрелки, но как насчет этого?

Чтобы лучше понять, давайте распределим первый бином через второй.

Хорошо, теперь мы можем выполнять сложение, складывая векторы после того, как мы выполнили преобразования. Давай попробуем.

Сначала у нас есть (3 + 2 i ) (1), что является (3 + 2 i ) масштабированным на 1.

Затем у нас есть (3 + 2 i ) (- 4 i ). Здесь происходят две вещи: масштабирование и вращение.

Сначала масштабируем его на 4, умножая (4) (3 + 2 i ), чтобы получить (12 + 8 i ).

Нам также нужно умножить на — i. Вызов умножение на — i — это поворот на 90˚ по часовой стрелке на .

Примечание: Это соответствует алгебре, которую мы вложили в i = √-1:

Последний шаг — выполнить сложение путем наложения векторов.

Наш окончательный ответ: 11-10 i .

Теперь вы можете подумать:

«Бретт, почему мы не можем просто решить это с помощью алгебры ??»

И это правда, мы можем решить эту проблему с помощью алгебры.Фактически, это наиболее эффективный способ решения проблемы (хотя в нем отсутствует понимание , которое вы получаете при построении графиков).

Я был бы паршивым математиком, если бы не показал вам оба пути. Итак, для всех моих друзей, любящих алгебру, вот как расширить и упростить вышеуказанную задачу:

Давайте разделим (3 + 2 i ) / (1–4 i ).

Здесь вы можете подумать, что можете просто разделить реальные части и мнимые части… но не так быстро.

Нет! Даже не думай об этом !!

Как и в алгебре, мы должны разделить знаменатель на оба члена числителя, что оставляет нас с той же проблемой:

Что на самом деле означает деление на комплексное число?

По правде говоря, это сбивает с толку, и этому нет хорошего объяснения.Было бы неплохо, если бы мы могли избавиться от мнимого числа в знаменателе ??

Хорошие новости → Именно этим мы и займемся!

Комплексное сопряжение

Ключ к решению этой проблемы — выяснить, как преобразовать знаменатель в простое действительное число.

Самый простой способ сделать это — использовать комплексный конъюгат .

Чтобы найти комплексное сопряжение, просто переверните знак у мнимой части. Например, комплексное сопряжение (1–4 i ) равно (1 + 4 i ).

Когда я умножаю их вместе, я получаю 17:

Конечно, я не могу просто умножить знаменатель на (1 + 4 i ). Как и любая дробь, если я хочу умножить знаменатель на значение, я должен также умножить числитель на это значение.

Теперь это имеет смысл. У нас есть два комплексных числа, которые умножаются в числителе, с которыми мы знаем, как обрабатывать из предыдущего раздела, и мы масштабируем все это на 1/17.

Вы можете решить это с помощью графика или воспользоваться сокращением алгебры:

Это было не так уж и плохо, не так ли?

Представление комплексных чисел на плоскости

Теперь, когда мы можем работать с комплексными числами и основными операциями: суммированием, вычитанием, умножением и делением, мы рассмотрим представление комплексных чисел на комплексной плоскости.Для действительных чисел мы рисовали прямую линию и располагали их в организованном порядке, как показано ниже:

Чтобы представить комплексные числа графически, мы должны нарисовать их на комплексной плоскости. Он образован действительной осью и мнимой осью. На действительной оси мы будем изображать действительную часть комплексного числа, а на мнимой оси — мнимую часть. Нарисуем указанную выше ось перпендикулярно и пересекающуюся в нуле, у которой действительная и мнимая части равны нулю.

Давайте посмотрим на пример комплексной плоскости:

Комплексное число $$ z $$ в биномной форме будет представлено в комплексной плоскости в следующем виде:

У нас есть комплекс $$ z = a + bi $$, где:

• $$ a $$ — любое действительное число, которое называется действительной частью $$ z $$.
• $$ b $$ — любое действительное число, которое называется мнимой частью $$ z $$.

Затем мы представляем $$ z = a + bi $$ на плоскости с вектором, связанным с $$ z $$, который является вектором с началом $$ (0,0) $$ и движется к точке $$ (а, б) $$.

Берем действительную часть комплексного числа и переносим ее на действительную ось. Берем мнимую часть и помещаем ее на мнимую ось. Мы проводим две линии, параллельные оси, в каждой из этих двух точек и ищем пересечение. Вектор, указывающий на пересечение этих прямых, представляет собой комплексное число $$ z $$.

Например, если мы хотим представить мнимое число $$ z = 2-i $$.

Сначала мы помещаем $$ 2 $$ на действительную ось.

Затем поместим $$ — i $$ на мнимую ось.

Рисуем две прямые:

Что мы делаем, так это ассоциируем вектор $$ (a, b) $$ с комплексным числом $$ z = a + bi $$ для графического представления $$ z $$.

Например, комплексное число $$ 3 + 9i $$ связано с вектором плоскости $$ (3,9) $$, а комплексное число $$ — 5i $$ связано с вектором $$ (0, — 5) $$.

Ранее мы говорили, что:

Мы определили сопряжение мнимого числа как число $$ \ bar {z} = a-ib $$.2} \ Big) $$.

Если нарисовать их в комплексной плоскости:

Геометрия комплексных чисел

Геометрия комплексных чисел

Комплексные числа могут быть представлены как в прямоугольных, так и в полярных координатах. Все комплексные числа можно записать в виде a + bi , где a и b — действительные числа, а i ² = −1. Каждое комплексное число соответствует точке на комплексной плоскости , когда точка с координатами ( a , b) связана с комплексным числом a + bi . В комплексной плоскости ось x называется действительной осью , а ось y называется мнимой осью .

Пример 1: График 4− 2 i −3 + 2 i и −5 -3 i в комплексной плоскости (см. Рисунок 1).

Рисунок 1
Комплексные числа на комплексной плоскости.

Комплексные числа можно преобразовать в полярные координаты с помощью соотношений x = r cos θ и y = r sin θ. Таким образом, если z — комплексное число:

Иногда выражение cos θ + sin θ записывается как cis θ. Абсолютное значение , или модуль , из z равно. Угол, образованный между положительной осью x и линией, проведенной от начала координат до z , называется аргументом или амплитудой z . Если z = x + iy — комплексное число, то сопряжение z записывается как z = x — iy

Пример 2: Преобразуйте комплексное число 5 — 3 i в полярные координаты (см. Рисунок 2).

Рисунок 2
Рисунок для примера 2.

Базовый угол θ ≈ 31 °.

Поскольку θ находится в четвертом квадранте,

Следовательно,

Чтобы найти произведение двух комплексных чисел, умножьте их абсолютные значения и сложите их амплитуды.

Чтобы найти частное двух комплексных чисел, разделите их абсолютные значения и вычтите их амплитуды.

Пример 3: Если z = a (cosα + i sinα) и w = b (cosβ + isinβ), то найдите их произведение zw .